Decision Trees for Regression

Neighborhoods via Recursive Partitioning

Objectives

In this note, we will discuss:

  • decision trees for regression,
  • how trees differ from KNN when determining similarity of data,
  • how to find and evaluate decision tree splits for regression,
  • and how to fit and tune decision trees with DecisionTreeRegressor.

We’ll return to the Auto MPG example to explore how trees split data and make predictions.

Python Setup

# basics
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns

# machine learning
from sklearn.datasets import make_friedman1, make_regression
from sklearn.tree import DecisionTreeRegressor, plot_tree, export_text
from sklearn.neighbors import KNeighborsRegressor
from sklearn.metrics import root_mean_squared_error, mean_squared_error, r2_score
from sklearn.model_selection import train_test_split

# data
from ucimlrepo import fetch_ucirepo

Notebook

The following Jupyter notebook contains some starter code that may be useful for following along with this note.

Introduction

Decision trees are a fundamental machine learning algorithm that can be used for both classification and regression tasks. In regression problems, decision trees predict numeric target variables by recursively partitioning the feature space into regions (“neighborhoods”) and predicting the mean (or other statistics like the median) of the target values within each region.

Loss Functions

\[ \text{MSE}(y, \hat{y}) = \frac{1}{n}\sum_{i=1}^{n} (y_i - \hat{y})^2 \]

\[ \text{MAE}(y, \hat{y}) = \frac{1}{n}\sum_{i=1}^{n} \left| (y_i - \hat{y}) \right| \]

\[ \text{SSE}(y, \hat{y}) = \sum_{i=1}^{n} (y_i - \hat{y})^2 \]

Tree Building Idea

\(x\) \(y\)
2.65 2.52
7.96 7.05
6.12 6.35
9.18 6.82
3.47 3.08
9.80 7.09
5.31 6.21
5.10 6.53
6.53 6.50
3.88 2.65
Table 1: Ten samples of simulated data with a single feature \(x\) and a target \(y\).

Decision trees split the feature data into regions (neighborhoods), called nodes, by finding optimal cutoffs.

Where KNN looks for neighbors when making predictions, decision trees create neighborhoods during fitting.

For a single feature \(x\) and node \(N\), we choose a cutoff value \(c_N\) that divides our data into two groups:

  • Left Node: \(N_L = \{i : x_i \leq c_N\}\)
  • Right Node: \(N_R = \{i : x_i > c_N\}\)

Each neighborhood predicts the mean of the target values within that region.

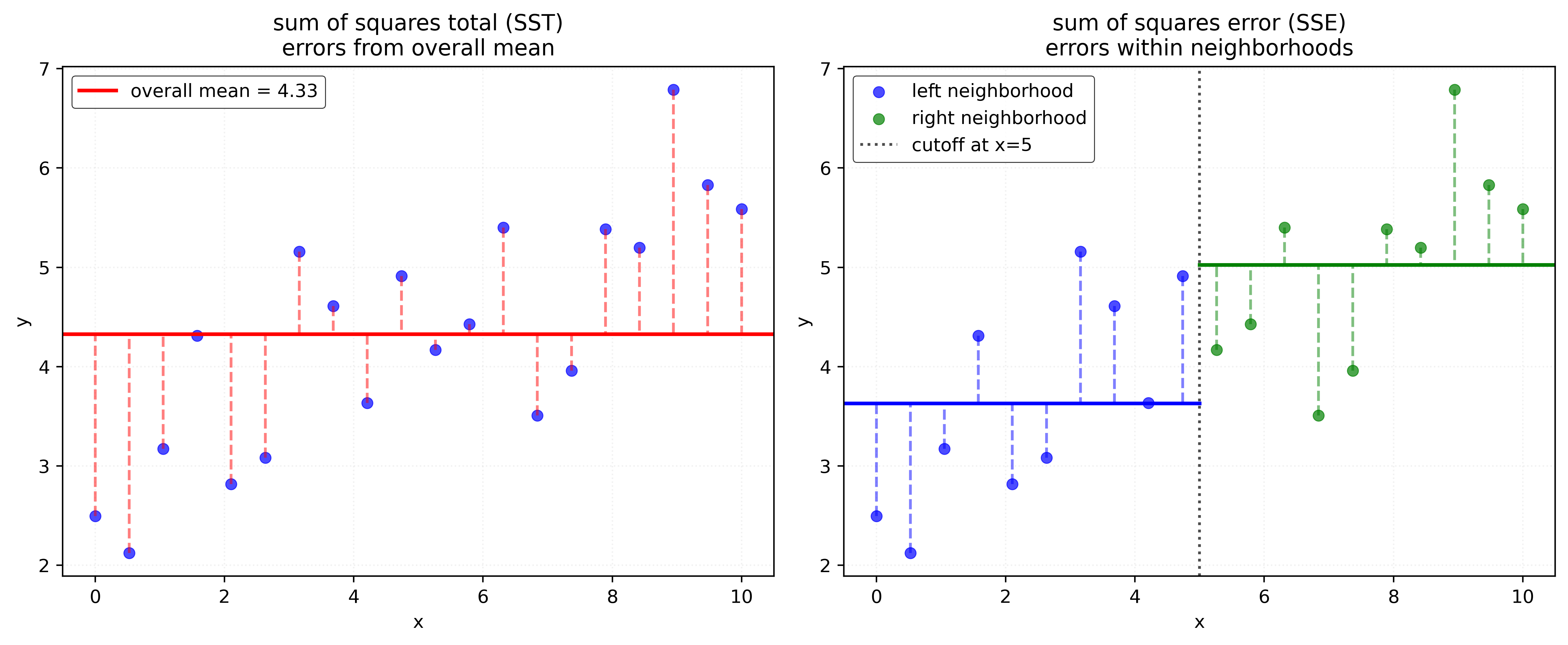
Figure 1: Comparison of SST vs SSE. Left panel shows SST (total sum of squares) with all residuals measured from the overall mean. Right panel shows SSE (sum of squared errors) after one split at x=5, with residuals measured from neighborhood means. The split reduces error by creating more homogeneous regions.

To find the optimal split, we consider all possible features (here just a single feature \(x\)) and all possible cutoff values, then choose the combination that minimizes \(\text{SSE}\).

After splitting node \(N\) based on \(x_j \leq c_N\), the new \(\text{SSE}\) is:

\[ \text{SSE}(y, \hat{y}) = \sum_{i=1}^{n} (y_i - \hat{y})^2 = \sum_{i \in N_L} (y_i - \bar{y}_L)^2 + \sum_{i \in N_R} (y_i - \bar{y}_R)^2 \]

where \(\bar{y}_L\) and \(\bar{y}_R\) are the means of the left and right nodes, respectively. That is, for samples in the left node, \(N_L\), the predicted value \(\hat{y}\) is \(\bar{y}_L\). For samples in the right node, \(N_R\), the predicted value \(\hat{y}\) is \(\bar{y}_R\).

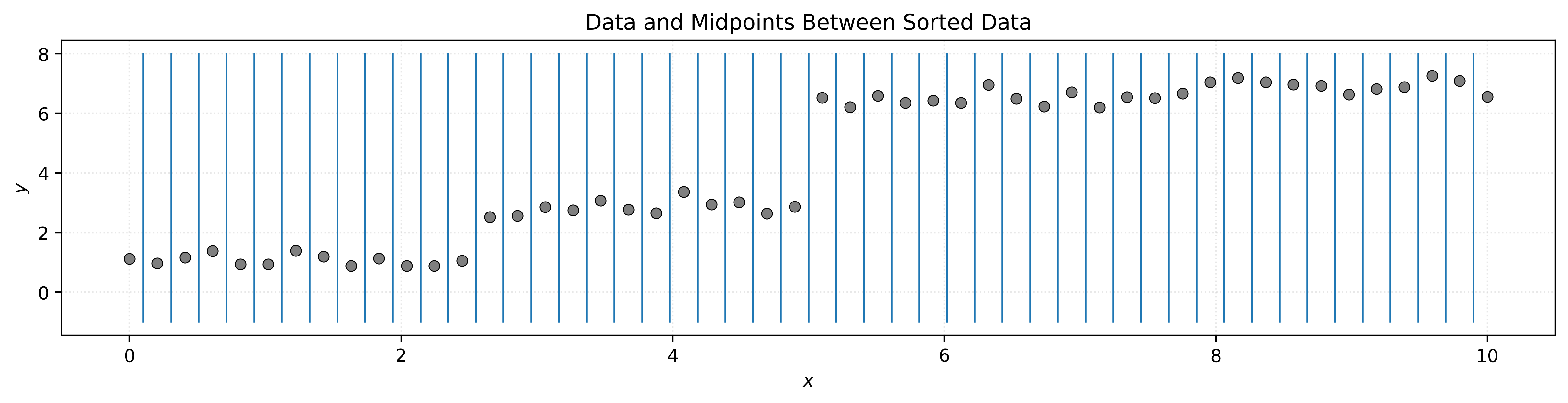
The algorithm considers all features and typically uses midpoints between adjacent sorted values as potential cutoffs.

A tree will consist of more than a single split. To develop a “deeper” tree, we recursively partition the feature space. That is, after splitting the root node \(N_0\) into nodes \(N_L\) and \(N_R\), we repeat the same process within both nodes.

We first split \(N_L\) into \(N_{LL}\) and \(N_{LR}\).

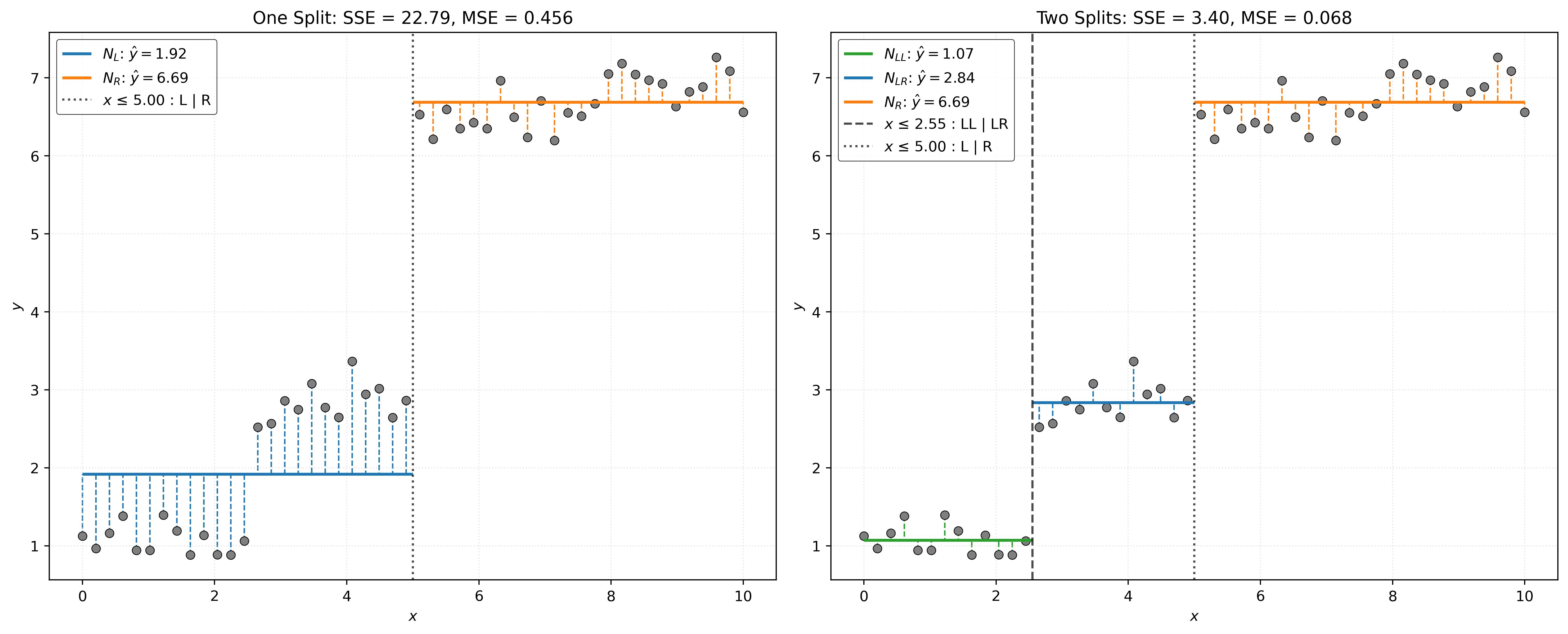
Figure 2: Progressive reduction of SSE through additional splits. Left panel shows one split at x=5 creating two neighborhoods. Right panel shows two splits (at x=2.5 and x=5) creating three neighborhoods. Each additional split reduces SSE by creating smaller, more homogeneous regions with shorter residuals.

With an arbitrary number of neighborhoods \(T\) (terminal nodes), we have:

\[ \text{SSE}(y, \hat{y}) = \sum_{t=1}^{T} \sum_{i \in N_t} (y_i - \bar{y}_t)^2 \]

We then split \(N_R\) into \(N_{RL}\) and \(N_{RR}\).

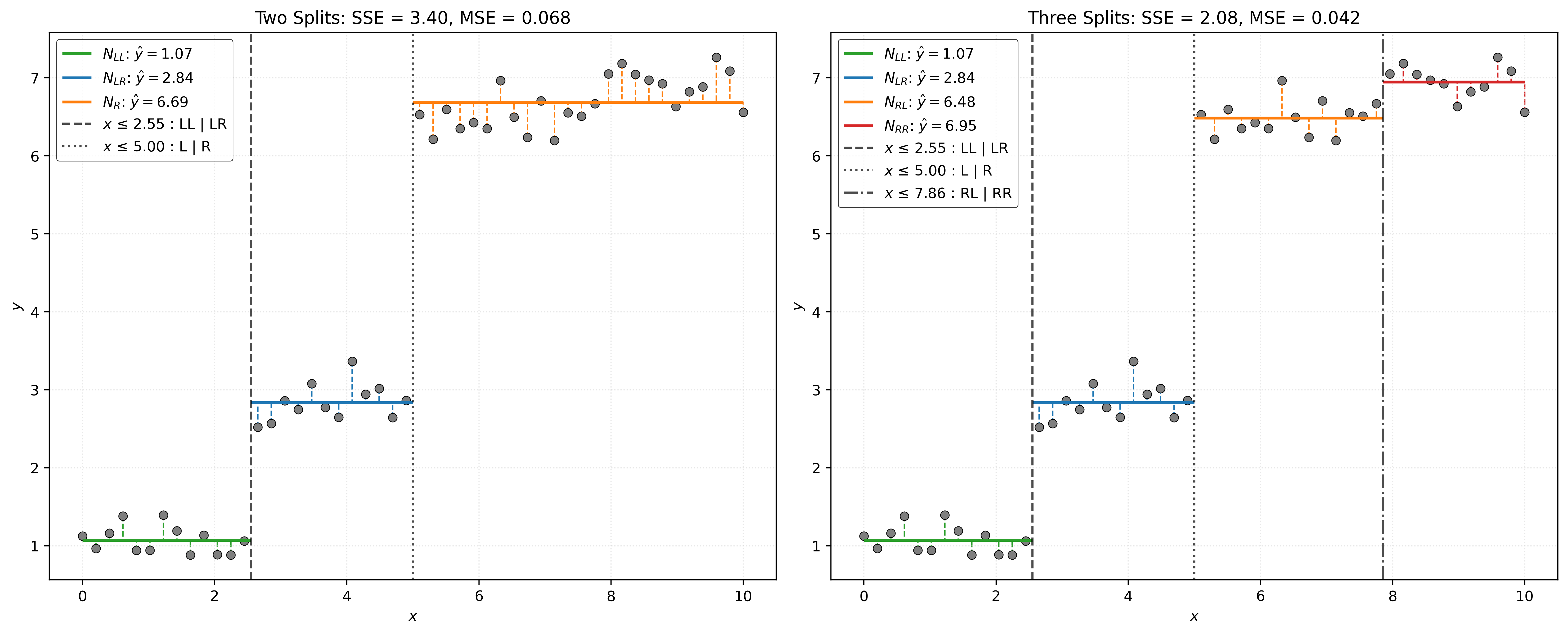
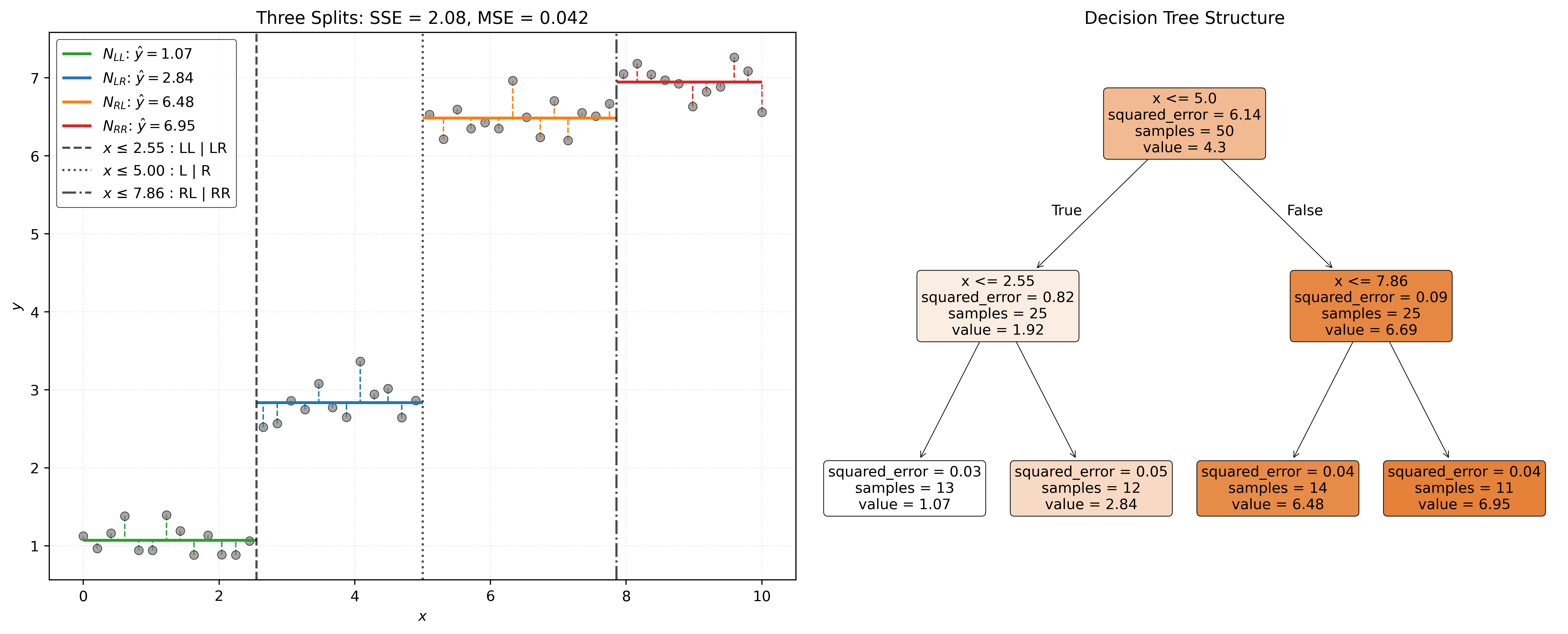
Figure 3: Adding a third split further reduces SSE. Left panel shows two splits creating three regions. Right panel shows three optimal splits creating four regions, each corresponding to our original step function levels.
Figure 4: Visualization of decision tree structure. Left panel shows the data with three splits creating four regions. Right panel shows the corresponding tree structure with decision nodes (splits) and leaf nodes (predictions).

With a tree build, we can give categorize the different types of nodes that we have encountered.

  • Root Node: The “top” node containing all data.
  • Terminal Nodes: Nodes at the “bottom” of the tree that are not split any further. In the tree analogy, this could also be called leaves.
  • Internal Nodes: Any node that is not the root node or a terminal node.

Decision Tree Tuning Parameters

def simulate_sin_data(n, sd, seed):
    np.random.seed(seed)
    X = np.random.uniform(
        low=-2 * np.pi,
        high=2 * np.pi,
        size=(n, 1),
    )
    signal = np.sin(X).ravel()
    noise = np.random.normal(
        loc=0,
        scale=sd,
        size=n,
    )
    y = signal + noise
    return X, y
X, y = simulate_sin_data(n=200, sd=0.25, seed=42)
Show Code for Plot 
# setup figure
fig, axs = plt.subplots(1, 2, figsize=(12, 5))

# x values to make predictions at for plotting purposes
x_plot = np.linspace(-2 * np.pi, 2 * np.pi, 1000).reshape((1000, 1))

# create subplot for "simulation study"
axs[0].set_title("Simulation Study")
axs[0].scatter(X, y, s=50, alpha=0.5, c="tab:gray")
axs[0].plot(x_plot, np.sin(x_plot), zorder=3)
axs[0].set_xlabel("$x$")
axs[0].set_ylabel("$y$")

# create subplot for "reality"
axs[1].set_title("Reality")
axs[1].scatter(X, y, s=50, alpha=0.5, c="tab:gray")
axs[1].set_xlabel("$x$")

# show plot
plt.show()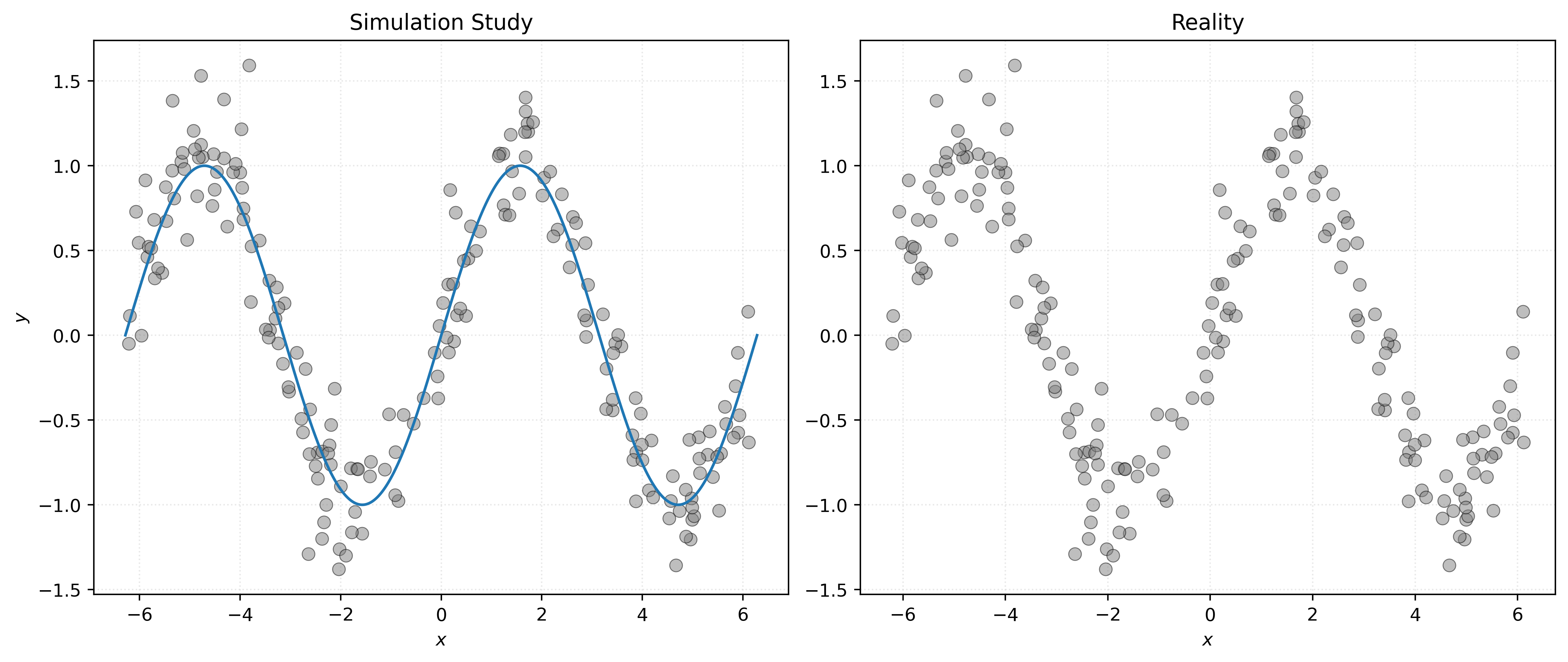
Figure 5: A visual representation of a data generating process, and data generated by the process. Left: A sine wave that is the signal and data generated by the process. Right: Data generated by the process, without any indication of the true signal. 
# fit a knn model for comparison
knn010 = KNeighborsRegressor(n_neighbors=10)
_ = knn010.fit(X, y)
# list the possible parameters (and their default values) to the DecisionTreeRegressor
DecisionTreeRegressor().get_params()
{'ccp_alpha': 0.0,
 'criterion': 'squared_error',
 'max_depth': None,
 'max_features': None,
 'max_leaf_nodes': None,
 'min_impurity_decrease': 0.0,
 'min_samples_leaf': 1,
 'min_samples_split': 2,
 'min_weight_fraction_leaf': 0.0,
 'monotonic_cst': None,
 'random_state': None,
 'splitter': 'best'}
# fit a decision tree with min_samples_split=40
dt040 = DecisionTreeRegressor(min_samples_split=40)
_ = dt040.fit(X, y)
Show Code for Plot 
# setup figure
fig, axs = plt.subplots(1, 2, figsize=(12, 5))

# create subplot for KNN
axs[0].set_title("k-Nearest Neighbors, $k=10$")
axs[0].scatter(X, y, s=50, alpha=0.5, c="tab:gray")
axs[0].plot(x_plot, knn010.predict(x_plot))
axs[0].set_xlabel("$x$")
axs[0].set_ylabel("$y$")

# create subplot for decision tree
axs[1].set_title(r"Decision Tree, $\mathtt{min\_samples\_split=40}$")
axs[1].scatter(X, y, s=50, alpha=0.5, c="tab:gray")
axs[1].plot(x_plot, dt040.predict(x_plot))
axs[0].set_xlabel("$x$")

# show plot
plt.show()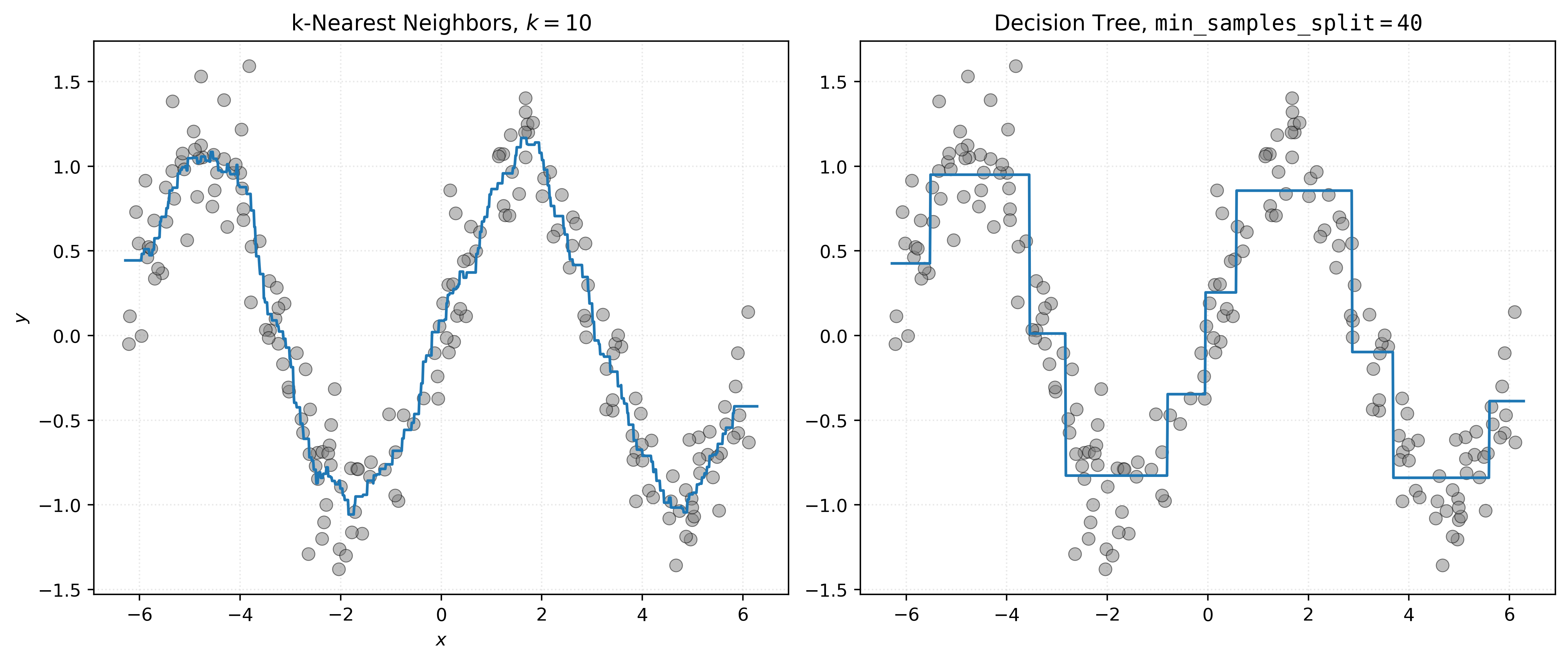

# visualize the decision tree
fig, ax = plt.subplots(1, 1, figsize=(12, 8))
plot_tree(dt040, feature_names=["x"], filled=True, rounded=True, fontsize=10, precision=2)
plt.show()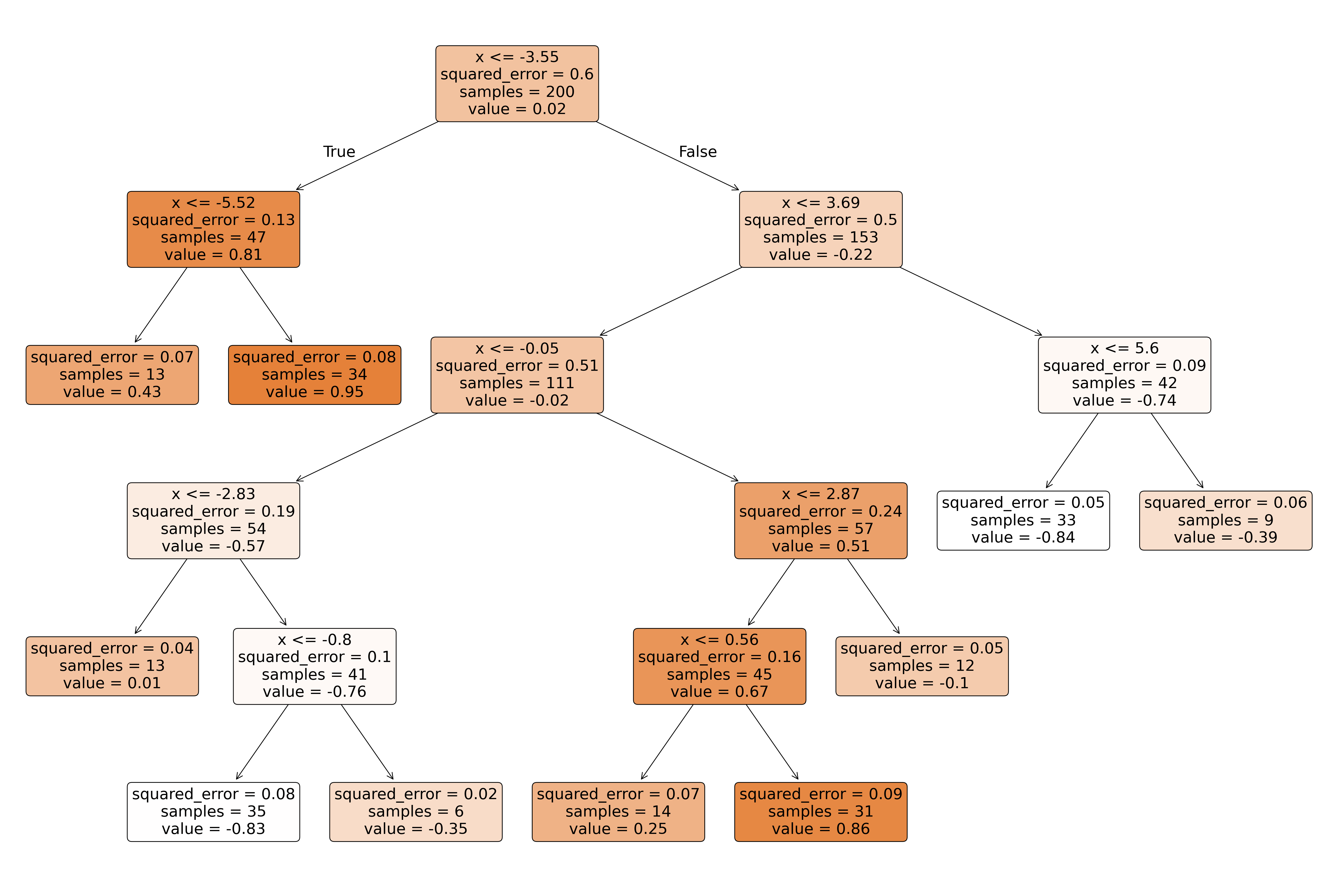

# view text representation of the tree
print(export_text(dt040))
|--- feature_0 <= -3.55
|   |--- feature_0 <= -5.52
|   |   |--- value: [0.43]
|   |--- feature_0 >  -5.52
|   |   |--- value: [0.95]
|--- feature_0 >  -3.55
|   |--- feature_0 <= 3.69
|   |   |--- feature_0 <= -0.05
|   |   |   |--- feature_0 <= -2.83
|   |   |   |   |--- value: [0.01]
|   |   |   |--- feature_0 >  -2.83
|   |   |   |   |--- feature_0 <= -0.80
|   |   |   |   |   |--- value: [-0.83]
|   |   |   |   |--- feature_0 >  -0.80
|   |   |   |   |   |--- value: [-0.35]
|   |   |--- feature_0 >  -0.05
|   |   |   |--- feature_0 <= 2.87
|   |   |   |   |--- feature_0 <= 0.56
|   |   |   |   |   |--- value: [0.25]
|   |   |   |   |--- feature_0 >  0.56
|   |   |   |   |   |--- value: [0.86]
|   |   |   |--- feature_0 >  2.87
|   |   |   |   |--- value: [-0.10]
|   |--- feature_0 >  3.69
|   |   |--- feature_0 <= 5.60
|   |   |   |--- value: [-0.84]
|   |   |--- feature_0 >  5.60
|   |   |   |--- value: [-0.39]

# initialize decision trees with different values of the tuning parameter min_samples_split
dt002 = DecisionTreeRegressor(min_samples_split=2)
dt100 = DecisionTreeRegressor(min_samples_split=100)
dt250 = DecisionTreeRegressor(min_samples_split=250)
# fit those models
_ = dt002.fit(X, y)
_ = dt100.fit(X, y)
_ = dt250.fit(X, y)
Show Code for Plot 
# setup figure
fig, axs = plt.subplots(1, 3, figsize=(18, 5))

# create subplot for decision tree with min_samples_split=250
axs[0].set_title(r"$\mathtt{min\_samples\_split=250}$")
axs[0].scatter(X, y, s=50, alpha=0.5, c="tab:gray")
axs[0].plot(x_plot, dt250.predict(x_plot))
axs[0].set_xlabel("$x$")
axs[0].set_ylabel("$y$")

# create subplot for decision tree with min_samples_split=100
axs[1].set_title(r"$\mathtt{min\_samples\_split=100}$")
axs[1].scatter(X, y, s=50, alpha=0.5, c="tab:gray")
axs[1].plot(x_plot, dt100.predict(x_plot))
axs[1].set_xlabel("$x$")

# create subplot for decision tree with min_samples_split=2
axs[2].set_title(r"$\mathtt{min\_samples\_split=2}$")
axs[2].scatter(X, y, s=50, alpha=0.5, c="tab:gray")
axs[2].plot(x_plot, dt002.predict(x_plot))
axs[2].set_xlabel("$x$")

# show plot
plt.show()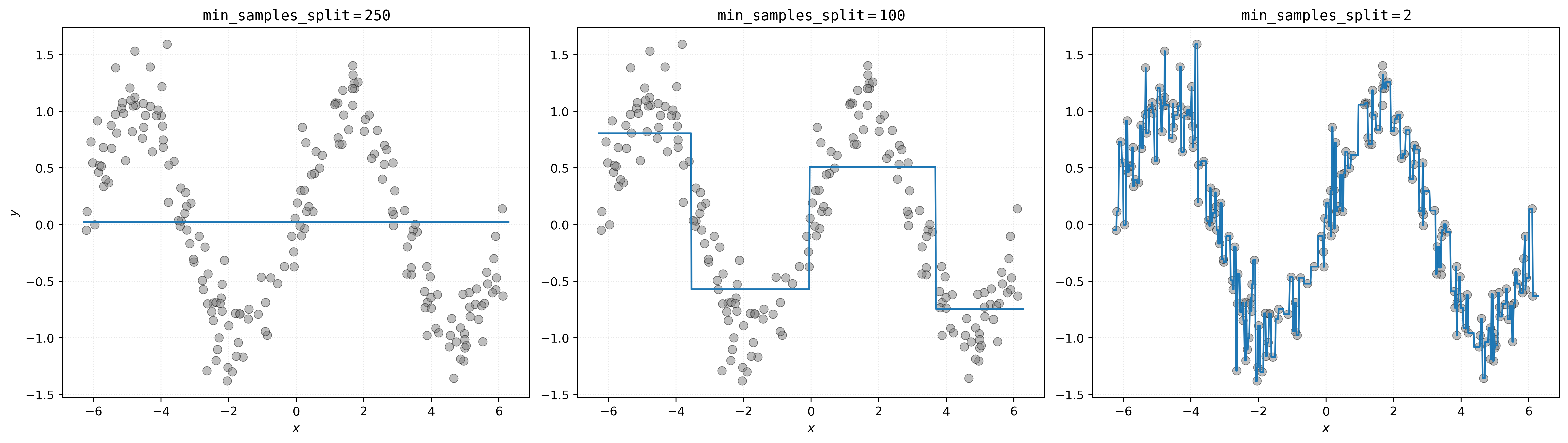

# initialize decision trees with different values of the tuning parameter max_depth
dt_d01 = DecisionTreeRegressor(max_depth=1)
dt_d05 = DecisionTreeRegressor(max_depth=5)
dt_d10 = DecisionTreeRegressor(max_depth=10)
# fit those models
_ = dt_d01.fit(X, y)
_ = dt_d05.fit(X, y)
_ = dt_d10.fit(X, y)
Show Code for Plot 
# setup figure
fig, axs = plt.subplots(1, 3, figsize=(18, 5))

# create subplot for decision tree with max_depth=1
axs[0].set_title(r"$\mathtt{max\_depth=1}$")
axs[0].scatter(X, y, s=50, alpha=0.5, c="tab:gray")
axs[0].plot(x_plot, dt_d01.predict(x_plot))
axs[0].set_xlabel("$x$")
axs[0].set_ylabel("$y$")

# create subplot for decision tree with max_depth=5
axs[1].set_title(r"$\mathtt{max\_depth=5}$")
axs[1].scatter(X, y, s=50, alpha=0.5, c="tab:gray")
axs[1].plot(x_plot, dt_d05.predict(x_plot))
axs[1].set_xlabel("$x$")

# create subplot for decision tree with max_depth=10
axs[2].set_title(r"$\mathtt{max\_depth=10}$")
axs[2].scatter(X, y, s=50, alpha=0.5, c="tab:gray")
axs[2].plot(x_plot, dt_d10.predict(x_plot))
axs[2].set_xlabel("$x$")

# show plot
plt.show()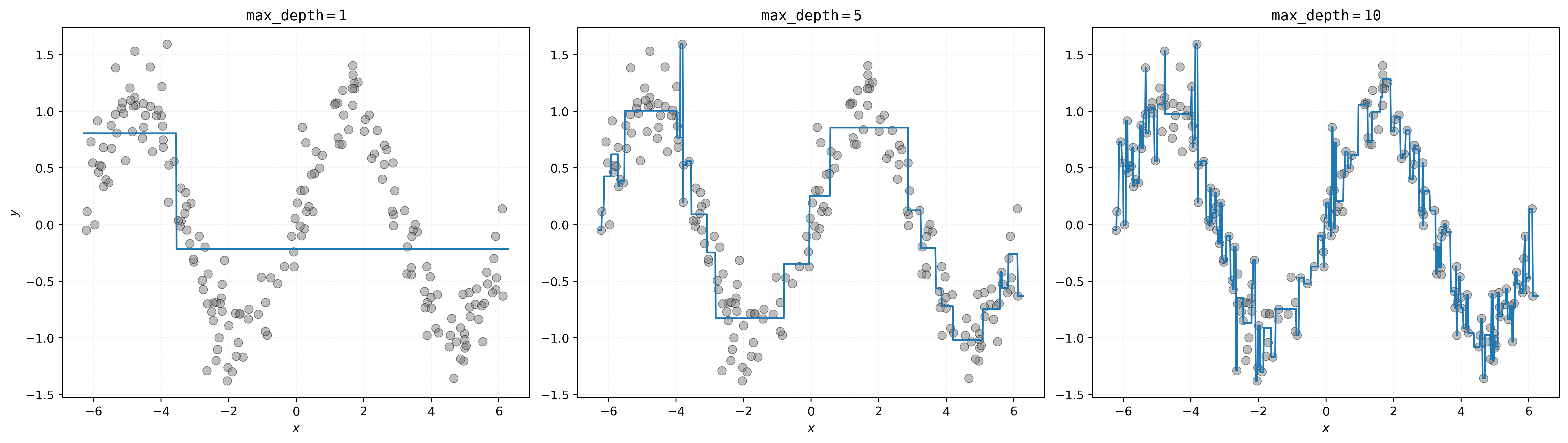

Recursive Partitioning Algorithm

The decision tree algorithm works through recursive partitioning. Let’s look at a sketch of the algorithm.

  • Initialize root node containing all data.
  • Set stop conditions via min_samples_split or max_depth.
  • While there are terminal nodes that can be split:
    • For each terminal node \(N\):
      • If stop conditions are met:
        • Skip node.
      • For each feature \(x_j\):
        • Find cutoff \(c_N\) for potential split \(x_j \leq c_N\) that minimizes loss (\(\text{SSE}\)).
      • Pick feature \(x_j\) (and associate cutoff \(c_N\)) with smallest loss.
      • Split \(N\) into \(N_L\) and \(N_R\) using \(x_j \leq c_N\), creating two new terminal nodes.

The algorithm considers all features and finds potential split points by examining the data. For continuous features, typical split points are the midpoints between adjacent unique values when the data is sorted.

Show Code for Recursive Partitioning Demo 
# create 2D dataset to show spatial partitioning
np.random.seed(307)
n = 100
x1 = np.random.uniform(0, 10, n)
x2 = np.random.uniform(0, 10, n)
y = 5 + 0.3 * x1 + 0.5 * x2 + 0.1 * x1 * x2 + np.random.normal(0, 2, n)

X = np.column_stack([x1, x2])

# fit trees with increasing depth
fig, axes = plt.subplots(2, 2, figsize=(12, 10))
axes = axes.ravel()

depths = [1, 2, 3, 4]
for i, depth in enumerate(depths):
    tree = DecisionTreeRegressor(max_depth=depth, random_state=42)
    tree.fit(X, y)

    # create prediction surface
    xx, yy = np.meshgrid(np.linspace(0, 10, 500), np.linspace(0, 10, 500))
    X_grid = np.column_stack([xx.ravel(), yy.ravel()])
    Z = tree.predict(X_grid).reshape(xx.shape)

    # plot the regions as discrete blocks (no interpolation)
    im = axes[i].imshow(
        Z,
        extent=[0, 10, 0, 10],
        origin="lower",
        cmap="coolwarm",
        aspect="equal",
        vmin=np.min(y),
        vmax=np.max(y),
    )
    scatter = axes[i].scatter(
        x1,
        x2,
        c=y,
        cmap="coolwarm",
    )
    axes[i].set_title(f"max_depth = {depth} ({tree.get_n_leaves()} leaves)")
    axes[i].set_xlabel("$x_1$")
    axes[i].set_ylabel("$x_2$")

    # add colorbar
    plt.colorbar(im, ax=axes[i], shrink=0.8)

# show plot
plt.show()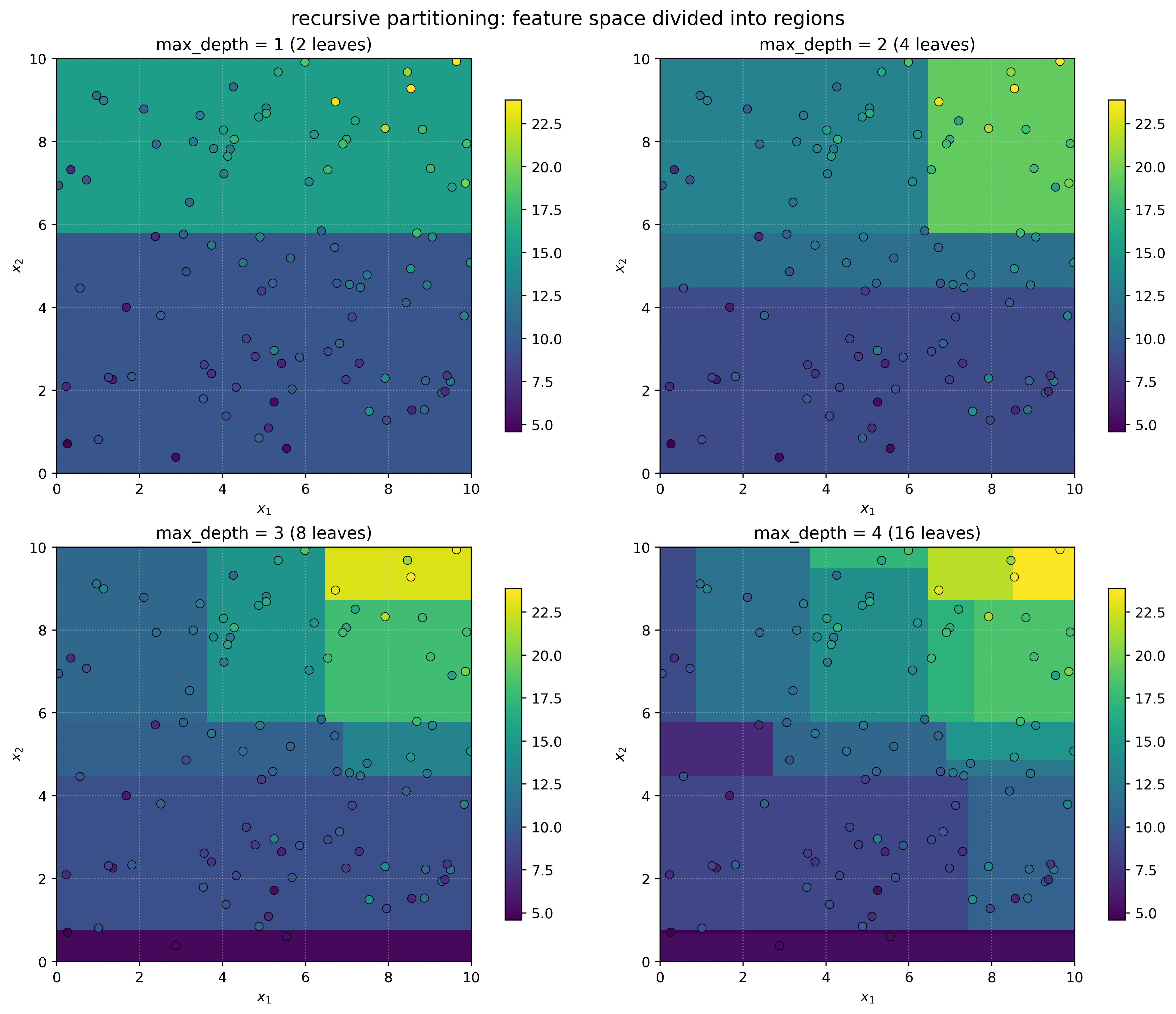
Figure 6: Demonstration of recursive partitioning process

Example: Automobile Fuel Efficiency

auto_mpg = fetch_ucirepo("Auto MPG")

We load the Auto MPG dataset using the fetch_ucirepo function, which provides access to datasets from the UCI Machine Learning Repository.

X = auto_mpg.data.features
y = auto_mpg.data.targets["mpg"]
X_train, X_test, y_train, y_test = train_test_split(
    X,
    y,
    test_size=0.2,
    random_state=42,
)
DecisionTreeRegressor().get_params()
{'ccp_alpha': 0.0,
 'criterion': 'squared_error',
 'max_depth': None,
 'max_features': None,
 'max_leaf_nodes': None,
 'min_impurity_decrease': 0.0,
 'min_samples_leaf': 1,
 'min_samples_split': 2,
 'min_weight_fraction_leaf': 0.0,
 'monotonic_cst': None,
 'random_state': None,
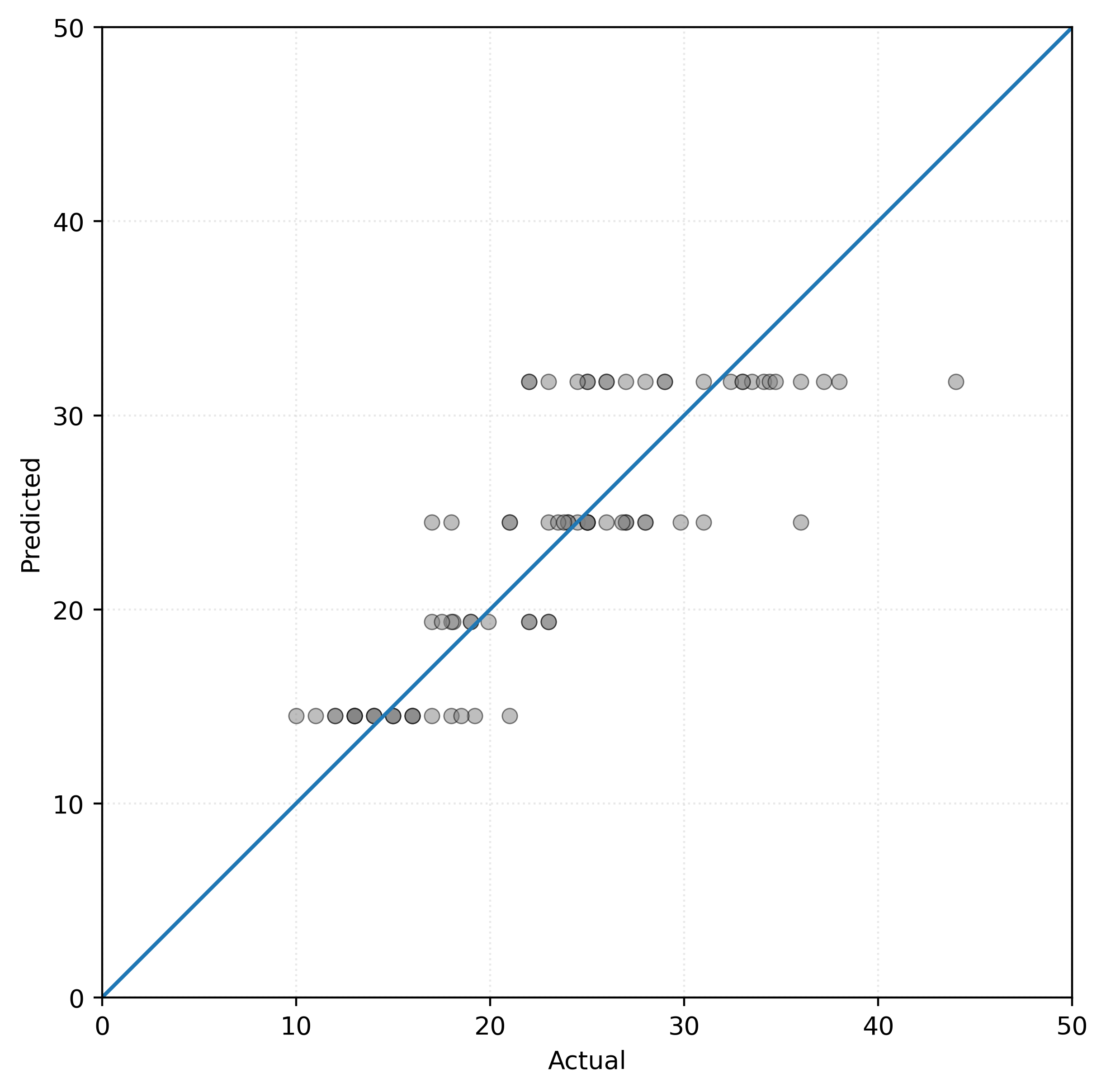
 'splitter': 'best'}
tree = DecisionTreeRegressor(max_depth=2, random_state=42)
_ = tree.fit(X_train, y_train)
tree.predict(X_test)
array([31.7385, 31.7385, 19.3635, 14.5213, 14.5213, 24.4915, 24.4915,
       14.5213, 19.3635, 14.5213, 14.5213, 31.7385, 31.7385, 14.5213,
       31.7385, 14.5213, 24.4915, 24.4915, 14.5213, 31.7385, 31.7385,
       19.3635, 19.3635, 31.7385, 14.5213, 31.7385, 24.4915, 24.4915,
       19.3635, 14.5213, 24.4915, 31.7385, 19.3635, 24.4915, 31.7385,
       14.5213, 24.4915, 14.5213, 14.5213, 31.7385, 24.4915, 31.7385,
       24.4915, 14.5213, 24.4915, 24.4915, 31.7385, 24.4915, 24.4915,
       31.7385, 31.7385, 31.7385, 31.7385, 14.5213, 24.4915, 14.5213,
       14.5213, 24.4915, 24.4915, 19.3635, 14.5213, 31.7385, 31.7385,
       24.4915, 19.3635, 24.4915, 24.4915, 31.7385, 31.7385, 14.5213,
       31.7385, 14.5213, 14.5213, 19.3635, 24.4915, 19.3635, 19.3635,
       24.4915, 31.7385, 14.5213])
fig, ax = plt.subplots()
plot_tree(tree, feature_names=X_train.columns, filled=True, rounded=True)
plt.show()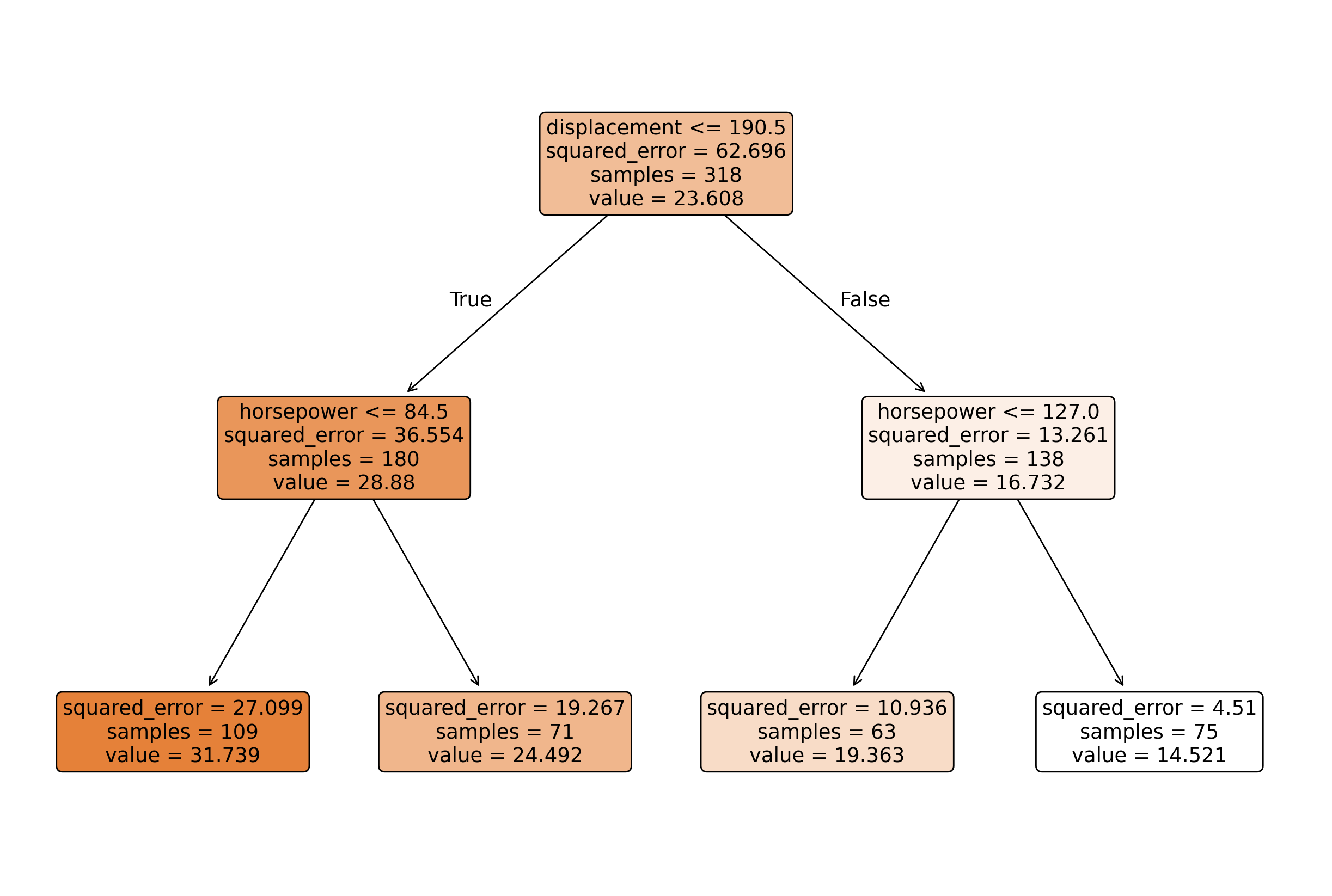

print(export_text(tree, feature_names=list(X_train.columns)))
|--- displacement <= 190.50
|   |--- horsepower <= 84.50
|   |   |--- value: [31.74]
|   |--- horsepower >  84.50
|   |   |--- value: [24.49]
|--- displacement >  190.50
|   |--- horsepower <= 127.00
|   |   |--- value: [19.36]
|   |--- horsepower >  127.00
|   |   |--- value: [14.52]
Show Code for Plot 
# setup figure
fig, ax = plt.subplots(figsize=(6, 6))

# create scatterplot
ax.scatter(y_test, tree.predict(X_test), alpha=0.50, c="tab:gray")
ax.axline((0, 0), slope=1)
ax.set_xlim(0, 50)
ax.set_ylim(0, 50)
ax.set_xlabel("Actual")
ax.set_ylabel("Predicted")
ax.set_aspect("equal")

# show figure
plt.show()

Back to top