# basics
import numpy as np
import matplotlib.pyplot as plt
# machine learning
from sklearn.datasets import make_friedman1
from sklearn.tree import DecisionTreeRegressor, plot_tree, export_text
from sklearn.neighbors import KNeighborsRegressor
from sklearn.metrics import root_mean_squared_errorDecision Trees
A Simple Nonparametric Model
Regression
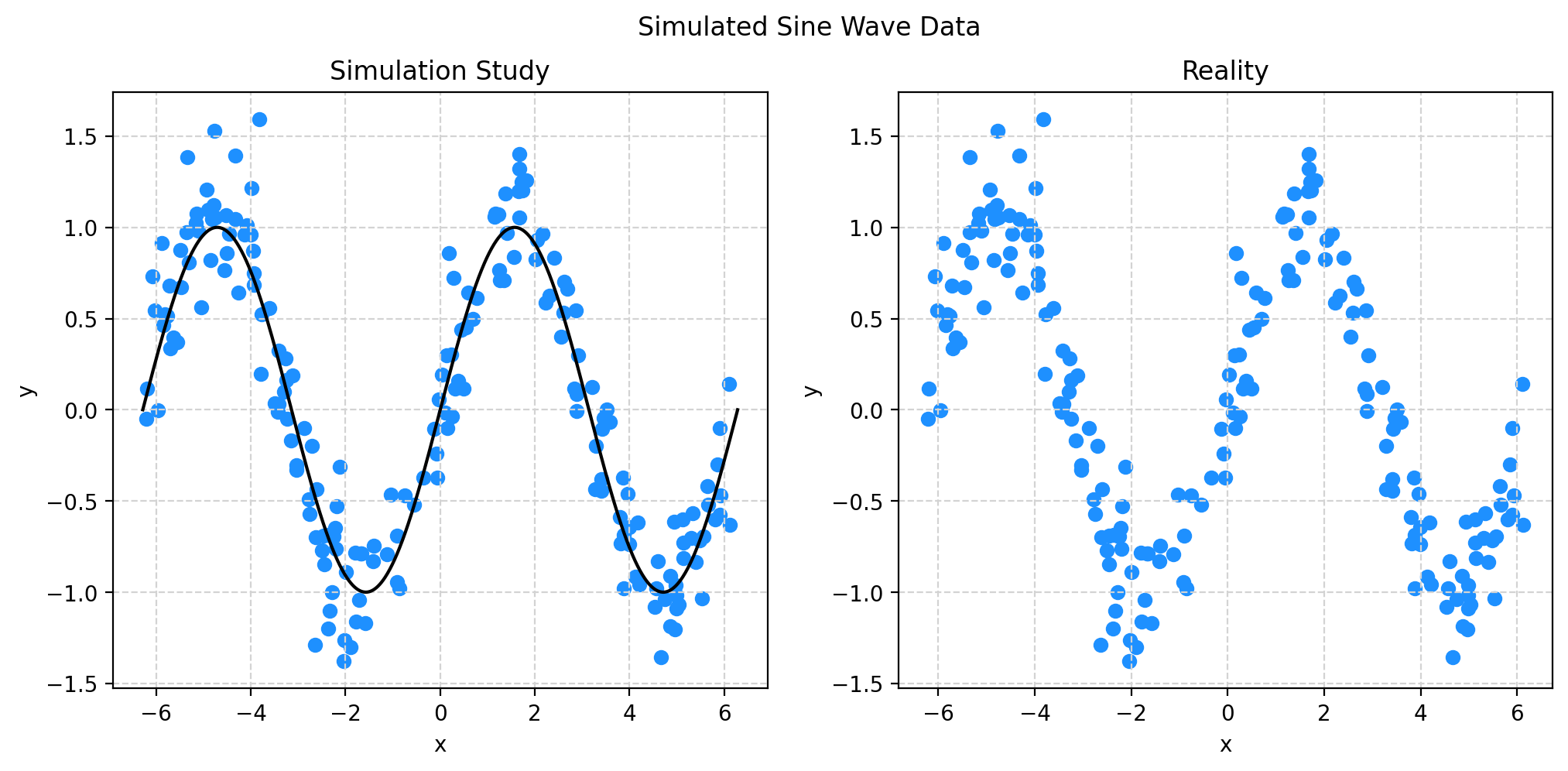
Simulated Sine Wave Data
# simulate sine wave data with numpy
np.random.seed(42)
n = 200
X = np.random.uniform(low=-2 * np.pi, high=2 * np.pi, size=(n, 1))
y = np.sin(X) + np.random.normal(loc=0, scale=0.25, size=(n, 1))# setup figure
fig, (ax1, ax2) = plt.subplots(1, 2)
fig.set_size_inches(12, 5)
fig.set_dpi(100)
# add overall title
fig.suptitle("Simulated Sine Wave Data")
# x values to make predictions at for plotting purposes
x_plot = np.linspace(-2 * np.pi, 2 * np.pi, 1000).reshape((1000, 1))
# create subplot for "simulation study"
ax1.set_title("Simulation Study")
ax1.scatter(X, y, color="dodgerblue")
ax1.set_xlabel("x")
ax1.set_ylabel("y")
ax1.grid(True, linestyle="--", color="lightgrey")
# add true regression function, the "signal" that we want to learn
ax1.plot(x_plot, np.sin(x_plot), color="black")
# create subplot for "reality"
ax2.set_title("Reality")
ax2.scatter(X, y, color="dodgerblue")
ax2.set_xlabel("x")
ax2.set_ylabel("y")
ax2.grid(True, linestyle="--", color="lightgrey")
# show plot
plt.show()# fit a knn model for comparison
knn010 = KNeighborsRegressor(n_neighbors=10)
_ = knn010.fit(X, y)# list the possible inputs (and their default values) to the DecisionTreeRegressor
DecisionTreeRegressor().get_params(){'ccp_alpha': 0.0,
'criterion': 'squared_error',
'max_depth': None,
'max_features': None,
'max_leaf_nodes': None,
'min_impurity_decrease': 0.0,
'min_samples_leaf': 1,
'min_samples_split': 2,
'min_weight_fraction_leaf': 0.0,
'monotonic_cst': None,
'random_state': None,
'splitter': 'best'}# fit a decision tree with min_samples_split=40
dt040 = DecisionTreeRegressor(min_samples_split=40)
_ = dt040.fit(X, y)# setup figure
fig, (ax1, ax2) = plt.subplots(1, 2)
fig.set_size_inches(12, 5)
fig.set_dpi(100)
# add overall title
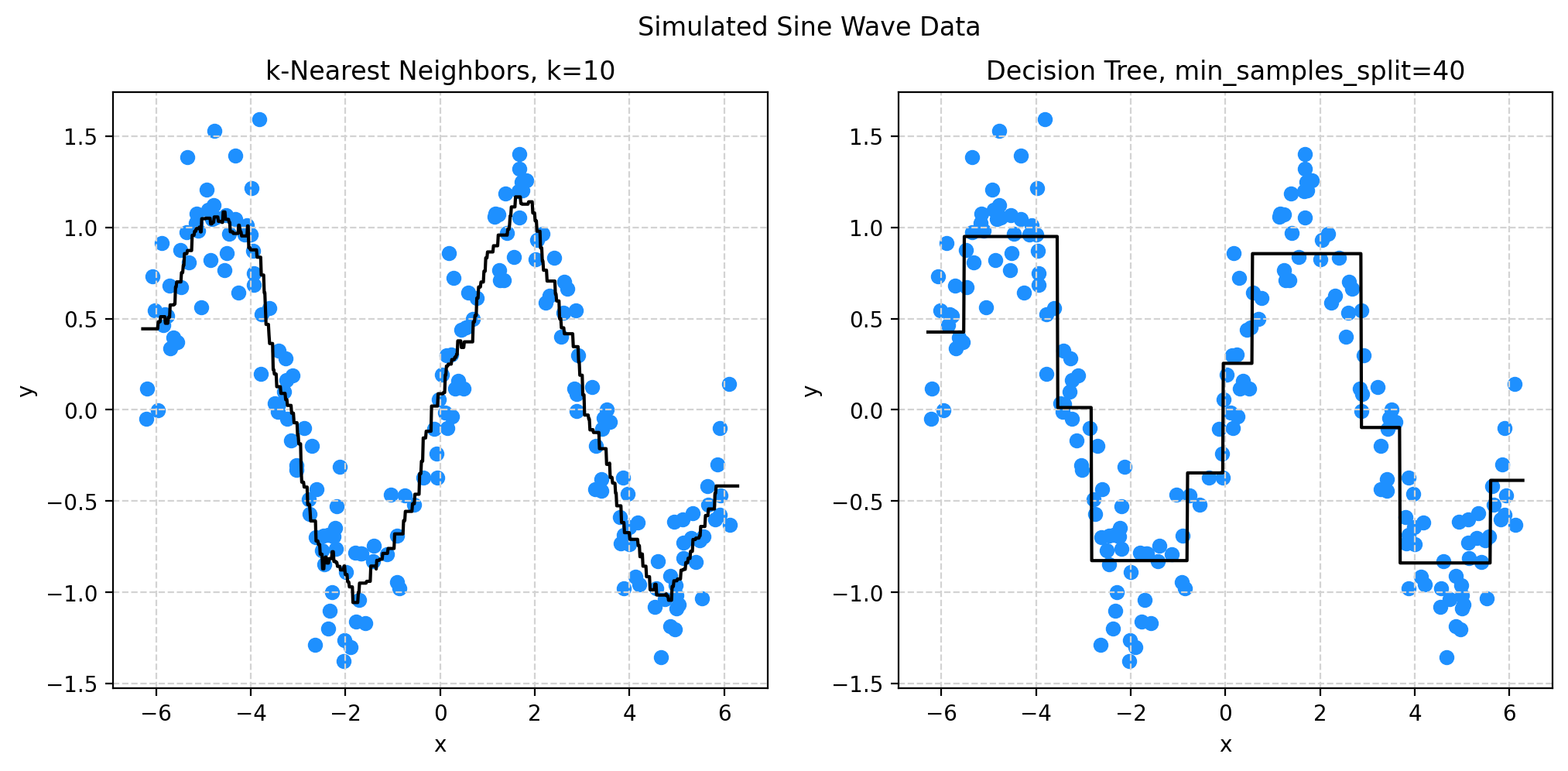
fig.suptitle("Simulated Sine Wave Data")
# x values to make predictions at for plotting purposes
x_plot = np.linspace(-2 * np.pi, 2 * np.pi, 1000).reshape((1000, 1))
# create subplot for KNN
ax1.set_title("k-Nearest Neighbors, k=10")
ax1.scatter(X, y, color="dodgerblue")
ax1.set_xlabel("x")
ax1.set_ylabel("y")
ax1.grid(True, linestyle="--", color="lightgrey")
ax1.plot(x_plot, knn010.predict(x_plot), color="black")
# create subplot for decision tree
ax2.set_title("Decision Tree, min_samples_split=40")
ax2.scatter(X, y, color="dodgerblue")
ax2.set_xlabel("x")
ax2.set_ylabel("y")
ax2.grid(True, linestyle="--", color="lightgrey")
ax2.plot(x_plot, dt040.predict(x_plot), color="black")
# show plot
plt.show()# visualize the decision tree
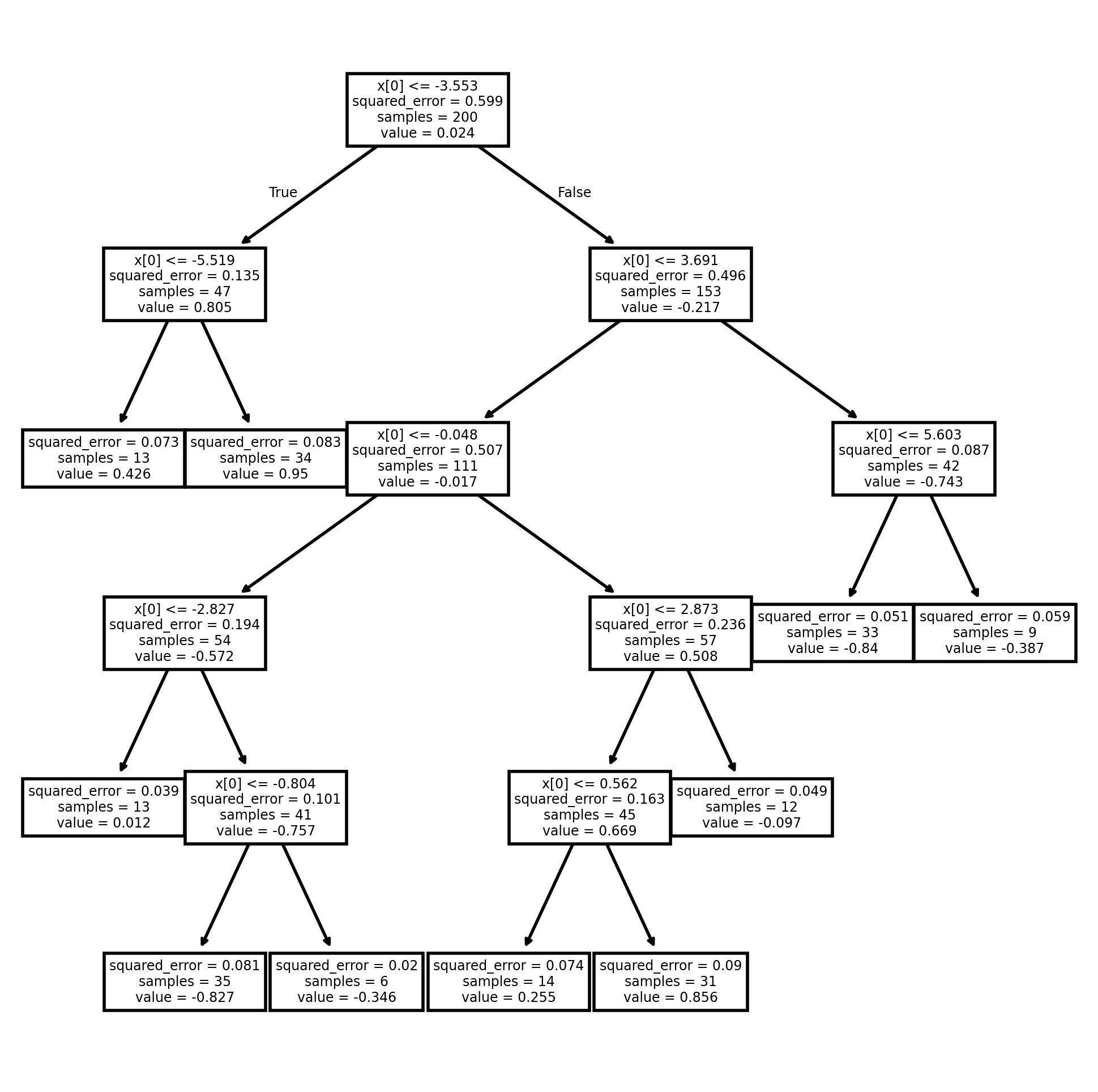
fig, ax = plt.subplots(1, 1)
fig.set_size_inches(6, 6)
fig.set_dpi(200)
plot_tree(dt040)
plt.show()# view text representation of the tree
print(export_text(dt040))|--- feature_0 <= -3.55
| |--- feature_0 <= -5.52
| | |--- value: [0.43]
| |--- feature_0 > -5.52
| | |--- value: [0.95]
|--- feature_0 > -3.55
| |--- feature_0 <= 3.69
| | |--- feature_0 <= -0.05
| | | |--- feature_0 <= -2.83
| | | | |--- value: [0.01]
| | | |--- feature_0 > -2.83
| | | | |--- feature_0 <= -0.80
| | | | | |--- value: [-0.83]
| | | | |--- feature_0 > -0.80
| | | | | |--- value: [-0.35]
| | |--- feature_0 > -0.05
| | | |--- feature_0 <= 2.87
| | | | |--- feature_0 <= 0.56
| | | | | |--- value: [0.25]
| | | | |--- feature_0 > 0.56
| | | | | |--- value: [0.86]
| | | |--- feature_0 > 2.87
| | | | |--- value: [-0.10]
| |--- feature_0 > 3.69
| | |--- feature_0 <= 5.60
| | | |--- value: [-0.84]
| | |--- feature_0 > 5.60
| | | |--- value: [-0.39]
# initialize decision trees with different values of the tuning parameter min_samples_split
dt002 = DecisionTreeRegressor(min_samples_split=2)
dt100 = DecisionTreeRegressor(min_samples_split=100)
dt250 = DecisionTreeRegressor(min_samples_split=250)# fit those models
_ = dt002.fit(X, y)
_ = dt100.fit(X, y)
_ = dt250.fit(X, y)# setup figure
fig, (ax1, ax2, ax3) = plt.subplots(1, 3)
fig.set_size_inches(18, 5)
fig.set_dpi(100)
# add overall title
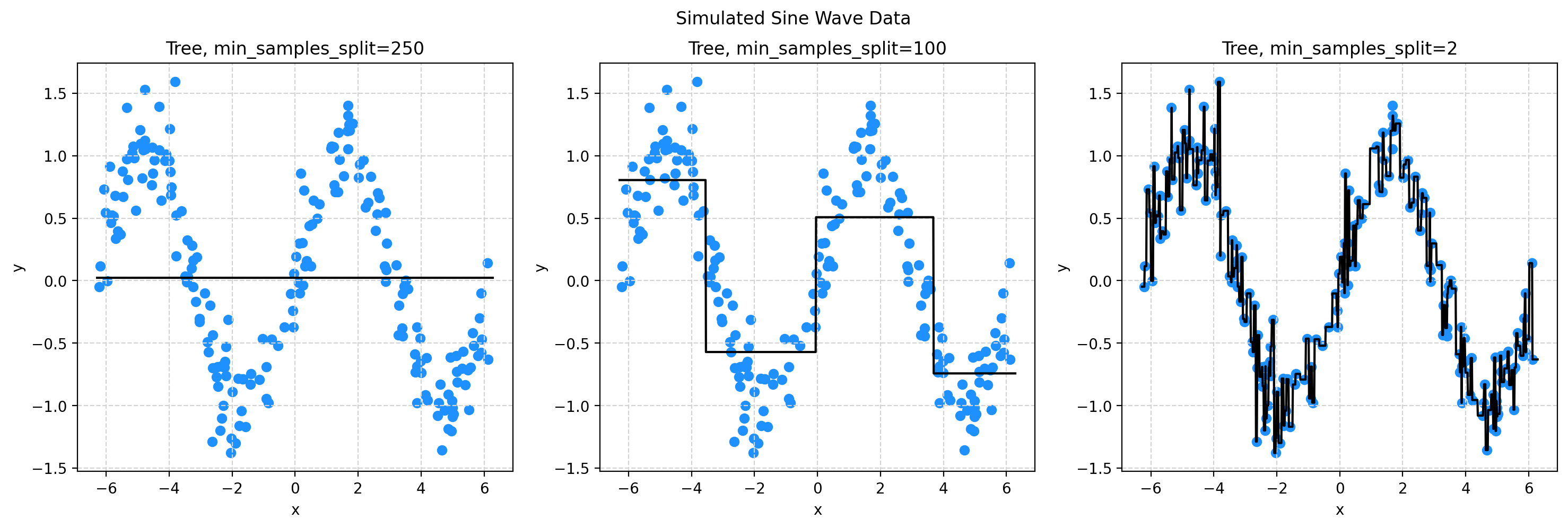
fig.suptitle("Simulated Sine Wave Data")
# x values to make predictions at for plotting purposes
x_plot = np.linspace(-2 * np.pi, 2 * np.pi, 1000).reshape((1000, 1))
# create subplot for decision tree with min_samples_split=250
ax1.set_title("Tree, min_samples_split=250")
ax1.scatter(X, y, color="dodgerblue")
ax1.set_xlabel("x")
ax1.set_ylabel("y")
ax1.grid(True, linestyle="--", color="lightgrey")
ax1.plot(x_plot, dt250.predict(x_plot), color="black")
# create subplot for decision tree with min_samples_split=100
ax2.set_title("Tree, min_samples_split=100")
ax2.scatter(X, y, color="dodgerblue")
ax2.set_xlabel("x")
ax2.set_ylabel("y")
ax2.grid(True, linestyle="--", color="lightgrey")
ax2.plot(x_plot, dt100.predict(x_plot), color="black")
# create subplot for decision tree with min_samples_split=2
ax3.set_title("Tree, min_samples_split=2")
ax3.scatter(X, y, color="dodgerblue")
ax3.set_xlabel("x")
ax3.set_ylabel("y")
ax3.grid(True, linestyle="--", color="lightgrey")
ax3.plot(x_plot, dt002.predict(x_plot), color="black")
# show plot
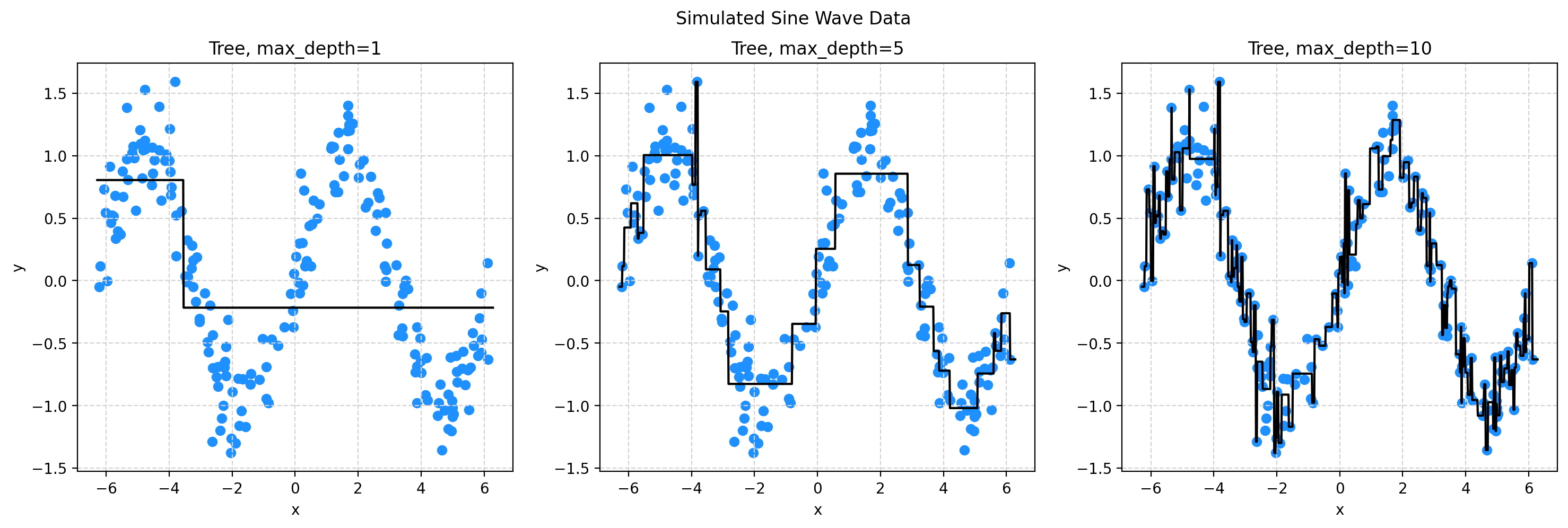
plt.show()# initialize decision trees with different values of the tuning parameter max_depth
dt_d01 = DecisionTreeRegressor(max_depth=1)
dt_d05 = DecisionTreeRegressor(max_depth=5)
dt_d10 = DecisionTreeRegressor(max_depth=10)# fit those models
_ = dt_d01.fit(X, y)
_ = dt_d05.fit(X, y)
_ = dt_d10.fit(X, y)# setup figure
fig, (ax1, ax2, ax3) = plt.subplots(1, 3)
fig.set_size_inches(18, 5)
fig.set_dpi(100)
# add overall title
fig.suptitle("Simulated Sine Wave Data")
# x values to make predictions at for plotting purposes
x_plot = np.linspace(-2 * np.pi, 2 * np.pi, 1000).reshape((1000, 1))
# create subplot for decision tree with max_depth=1
ax1.set_title("Tree, max_depth=1")
ax1.scatter(X, y, color="dodgerblue")
ax1.set_xlabel("x")
ax1.set_ylabel("y")
ax1.grid(True, linestyle="--", color="lightgrey")
ax1.plot(x_plot, dt_d01.predict(x_plot), color="black")
# create subplot for decision tree with max_depth=5
ax2.set_title("Tree, max_depth=5")
ax2.scatter(X, y, color="dodgerblue")
ax2.set_xlabel("x")
ax2.set_ylabel("y")
ax2.grid(True, linestyle="--", color="lightgrey")
ax2.plot(x_plot, dt_d05.predict(x_plot), color="black")
# create subplot for decision tree with max_depth=10
ax3.set_title("Tree, max_depth=10")
ax3.scatter(X, y, color="dodgerblue")
ax3.set_xlabel("x")
ax3.set_ylabel("y")
ax3.grid(True, linestyle="--", color="lightgrey")
ax3.plot(x_plot, dt_d10.predict(x_plot), color="black")
# show plot
plt.show()Simulated Data with Multiple Features
# simulate and inspect data
X_train, y_train = make_friedman1(n_samples=200, n_features=5, random_state=42)
X_test, y_test = make_friedman1(n_samples=200, n_features=5, random_state=1)
X_train[:10]array([[0.37454012, 0.95071431, 0.73199394, 0.59865848, 0.15601864],
[0.15599452, 0.05808361, 0.86617615, 0.60111501, 0.70807258],
[0.02058449, 0.96990985, 0.83244264, 0.21233911, 0.18182497],
[0.18340451, 0.30424224, 0.52475643, 0.43194502, 0.29122914],
[0.61185289, 0.13949386, 0.29214465, 0.36636184, 0.45606998],
[0.78517596, 0.19967378, 0.51423444, 0.59241457, 0.04645041],
[0.60754485, 0.17052412, 0.06505159, 0.94888554, 0.96563203],
[0.80839735, 0.30461377, 0.09767211, 0.68423303, 0.44015249],
[0.12203823, 0.49517691, 0.03438852, 0.9093204 , 0.25877998],
[0.66252228, 0.31171108, 0.52006802, 0.54671028, 0.18485446]])# initialize, fit, and evaluate a decision tree
dt = DecisionTreeRegressor(min_samples_split=50)
_ = dt.fit(X_train, y_train)
dt_pred = dt.predict(X_test)
print(root_mean_squared_error(y_test, dt_pred))3.0156480081689834# visualize the decision tree
fig, ax = plt.subplots(1, 1)
fig.set_size_inches(6, 6)
fig.set_dpi(200)
plot_tree(dt)
plt.show()# view text representation of the tree
print(export_text(dt))|--- feature_3 <= 0.43
| |--- feature_0 <= 0.28
| | |--- value: [7.48]
| |--- feature_0 > 0.28
| | |--- feature_1 <= 0.22
| | | |--- value: [6.74]
| | |--- feature_1 > 0.22
| | | |--- value: [13.35]
|--- feature_3 > 0.43
| |--- feature_0 <= 0.24
| | |--- value: [12.57]
| |--- feature_0 > 0.24
| | |--- feature_1 <= 0.33
| | | |--- value: [15.82]
| | |--- feature_1 > 0.33
| | | |--- feature_3 <= 0.78
| | | | |--- value: [17.72]
| | | |--- feature_3 > 0.78
| | | | |--- value: [21.46]
Classification
# basics
import numpy as np
# machine learning
from sklearn.datasets import make_blobs
from sklearn.tree import DecisionTreeClassifier, plot_tree, export_text
from sklearn.neighbors import KNeighborsClassifier
from sklearn.preprocessing import StandardScaler# simulate train data
X_train, y_train = make_blobs(
n_samples=201,
n_features=2,
cluster_std=3.75,
centers=3,
random_state=42,
)# simulate test data
X_test, y_test = make_blobs(
n_samples=201,
n_features=2,
cluster_std=3.75,
centers=3,
random_state=42,
)# list the possible inputs (and their default values) to the DecisionTreeClassifier
# these are all tuneable
DecisionTreeClassifier().get_params(){'ccp_alpha': 0.0,
'class_weight': None,
'criterion': 'gini',
'max_depth': None,
'max_features': None,
'max_leaf_nodes': None,
'min_impurity_decrease': 0.0,
'min_samples_leaf': 1,
'min_samples_split': 2,
'min_weight_fraction_leaf': 0.0,
'monotonic_cst': None,
'random_state': None,
'splitter': 'best'}# initialize a decision tree
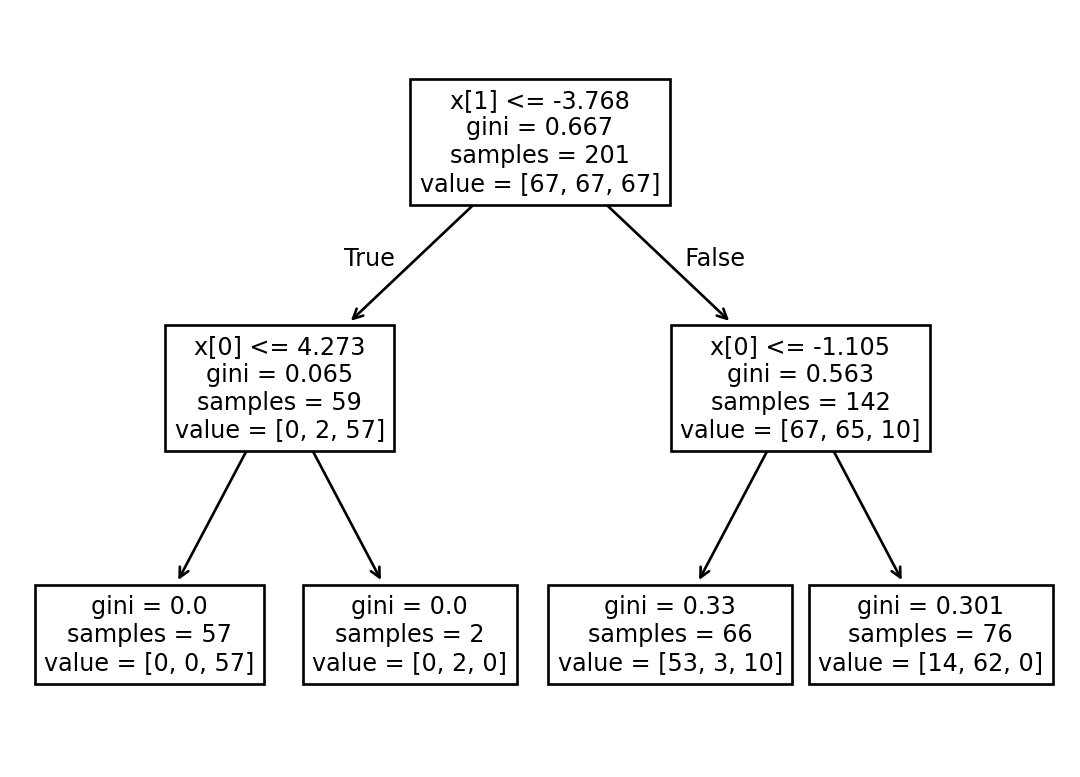
tree = DecisionTreeClassifier(max_depth=2)# fit the decision tree
_ = tree.fit(X_train, y_train)# calculate test accuracy
np.mean(tree.predict(X_test) == y_test)0.8656716417910447# inspect (first 10) estimated conditional probabilities in test data
tree.predict_proba(X_test)[:10]array([[0. , 0. , 1. ],
[0.8030303 , 0.04545455, 0.15151515],
[0.18421053, 0.81578947, 0. ],
[0.18421053, 0.81578947, 0. ],
[0.18421053, 0.81578947, 0. ],
[0.18421053, 0.81578947, 0. ],
[0.18421053, 0.81578947, 0. ],
[0. , 0. , 1. ],
[0. , 0. , 1. ],
[0.18421053, 0.81578947, 0. ]])# view text representation of the tree
print(export_text(tree, show_weights=True))|--- feature_1 <= -3.77
| |--- feature_0 <= 4.27
| | |--- weights: [0.00, 0.00, 57.00] class: 2
| |--- feature_0 > 4.27
| | |--- weights: [0.00, 2.00, 0.00] class: 1
|--- feature_1 > -3.77
| |--- feature_0 <= -1.11
| | |--- weights: [53.00, 3.00, 10.00] class: 0
| |--- feature_0 > -1.11
| | |--- weights: [14.00, 62.00, 0.00] class: 1
Effects of Scaling
# simulate train data
X_train, y_train = make_blobs(
n_samples=201,
n_features=2,
cluster_std=3.75,
centers=3,
random_state=42,
)
# modify a feature to but it on a very different scale
X_train[:, 1] = X_train[:, 1] * 20# simulate test data
X_test, y_test = make_blobs(
n_samples=201,
n_features=2,
cluster_std=3.75,
centers=3,
random_state=42,
)
# modify a feature to but it on a very different scale
X_test[:, 1] = X_test[:, 1] * 20# inspect the train data
X_train[:10]array([[-5.96100255e+00, -1.75622930e+02],
[-2.13550500e+00, 1.42525049e+02],
[ 1.72490722e-01, 8.87049143e+01],
[ 1.31367044e-03, -5.95708523e+01],
[ 6.24031968e-01, 7.56488248e+01],
[ 1.07614212e+01, -6.77972097e+01],
[ 4.81077324e+00, -9.40663239e+00],
[-9.32064131e-01, -2.30438354e+02],
[-3.83139425e+00, -9.03800287e+01],
[ 1.16388957e+00, 3.49989920e+01]])# learn scaler from train data and transform both train and test X data
scaler = StandardScaler()
scaler.fit(X_train)
X_train_transformed = scaler.transform(X_train)
X_test_transformed = scaler.transform(X_test)# create tree and knn models
tree = DecisionTreeClassifier(max_depth=10)
knn = KNeighborsClassifier()# scaling has an effect on knn!
_ = knn.fit(X_train, y_train)
print(knn.predict(X_test[:25, :]))
_ = knn.fit(X_train_transformed, y_train)
print(knn.predict(X_test_transformed[:25, :]))[2 0 0 1 0 1 1 2 2 0 1 0 0 1 2 0 2 2 2 2 1 1 1 1 0]
[2 0 1 1 1 1 1 2 2 1 2 0 2 1 2 0 2 2 2 2 1 1 0 1 0]# scaling has no effect on trees!
_ = tree.fit(X_train, y_train)
print(tree.predict(X_test[:25, :]))
_ = tree.fit(X_train_transformed, y_train)
print(tree.predict(X_test_transformed[:25, :]))[2 0 1 1 1 1 1 2 2 1 2 0 2 1 2 0 2 2 2 2 1 1 0 1 0]
[2 0 1 1 1 1 1 2 2 1 2 0 2 1 2 0 2 2 2 2 1 1 0 1 0]