Logistic Regression

A Parametric Classification Model

Author

David Dalpiaz

Modified

March 14, 2025

This note is still under construction, but should contain all necessary and relevant formulas and example code.

# basics
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap

# machine learning
from sklearn.datasets import make_blobs, make_circles
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.inspection import DecisionBoundaryDisplay
from sklearn.metrics import accuracy_score

Despite the name logistic regression, in a machine learning context logistic regression is a classification model.

This discrepancy arises due to logistic regression’s strong ties to generalized linear models developed by the field of statistics. In statistics, regression is a broad term used to describe any estimation of a statistical functional of a conditional distribution.

Binary Classification Setup

Logistic regression is a model for a binary target. Recall that in a binary setting, we often encode the target as \(Y \in \{0, 1\}\). Because we are mostly concerned with \(P[Y = 1 \mid \pmb{X} = \pmb{x}]\), we define a useful shorthand notation.

\[ p(\pmb{x}) = P[Y = 1 \mid \pmb{X} = \pmb{x}] \]

\[ P[Y = 0 \mid \pmb{X} = \pmb{x}] + P[Y = 1 \mid \pmb{X} = \pmb{x}] = 1 \]

\[ 1 - p(\pmb{x}) = P[Y = 0 \mid \pmb{X} = \pmb{x}] \]

Logistic Regression Model

\[ \log\left(\frac{p(\pmb{x})}{1 - p(\pmb{x})}\right) = \beta_0 + \beta_1 x_1 + \ldots + \beta_p x_p \]

\[ \frac{p(\pmb{x})}{1 - p(\pmb{x})} = \frac{P[Y = 1 \mid \pmb{X} = \pmb{x}]}{P[Y = 0 \mid \pmb{X} = \pmb{x}]} \]

\[ p(\pmb{x}) = P[Y = 1 \mid \pmb{X} = \pmb{x}] = \frac{e^{\beta_0 + \beta_1 x_{1} + \cdots + \beta_p x_p}}{1 + e^{\beta_0 + \beta_1 x_{1} + \cdots + \beta_p x_p}} \]

\[ \text{logit}(\xi) = \log\left(\frac{\xi}{1 - \xi}\right) \]

\[ \sigma(\xi) = \text{logit}^{-1}(\xi) = \frac{e^\xi}{1 + e^{\xi}} = \frac{1}{1 + e^{-\xi}} \]

\[ \eta(\pmb{x}) = \beta_0 + \beta_1 x_1 + \ldots + \beta_p x_p \]

\[ \log\left(\frac{p(\pmb{x})}{1 - p(\pmb{x})}\right) = \eta(\pmb{x}) \]

Whenever you hear “logarithm” or “log” you should assume this means the natural logarithm, unless specified otherwise. Make this assumption even if it is written as \(\log\) and not \(\ln\) as you might have seen previously.

The notion that \(\log\) without any qualifier could be considered a base 10 logarithm is a bad habit. When speaking with mathematicians or statisticians, they are almost exclusively using natural logarithms so they won’t bother to qualify what they mean by \(\log\) and you should assume they mean natural logarithm.1

\[ p(\pmb{x}) = \sigma(\eta(\pmb{x})) = \frac{e^{\eta(\pmb{x})}}{1 + e^{\eta(\pmb{x})}} = \frac{1}{1 + e^{-\eta(\pmb{x})}} = \frac{1}{1 + e^{-(\beta_0 + \beta_1 x_1 + \ldots + \beta_p x_p)}} \]

\[ Y \mid \pmb{X} = \pmb{x} \sim \text{Bernoulli}(p(\pmb{x})) \]

Examples in Python

# helper function to convert numpy (two column) X and y to a pandas df
# useful for printing and plotting
def numpy_to_df(X, y):
    df = pd.DataFrame(
        {
            "x1": X[:, 0],
            "x2": X[:, 1],
            "y": y,
        }
    )
    return df
# helper function to create a custom decision region plot
def plot_decision_regions(mod, X, y):

    # define colors for points
    illini_cmap = ListedColormap(
        [
            "#1D58A7",  # illini industrial blue
            "#FF5F05",  # illini orange
        ]
    )

    # define colors for decision regions
    light_illini_cmap = ListedColormap(
        [
            "#BFC9D9",  # illini industrial blue (lighter)
            "#FCCFB5",  # a lighter orange
        ]
    )

    # create figure and axes
    _, ax = plt.subplots(figsize=(8, 6))

    # start with sklearn default plot
    DecisionBoundaryDisplay.from_estimator(
        mod,
        X,
        cmap=light_illini_cmap,
        ax=ax,
        grid_resolution=1000,
        response_method="predict",
        plot_method="pcolormesh",
        shading="auto",
        xlabel="$x_1$",
        ylabel="$x_2$",
    )

    # add points to plot
    for i, shape in enumerate(["o", "s"]):
        mask = y == i
        ax.scatter(
            X[mask, 0],
            X[mask, 1],
            color=illini_cmap(i),
            edgecolors="white",
            linewidth=1,
            marker=shape,
            label=f"Class {i}",
        )

    # add title and legend
    _ = ax.set_title("Logistic Regression Decision Boundary")
    _ = ax.legend(loc="best")

    # show plot
    plt.show()
# make "blob" data for classification
X, y = make_blobs(
    n_samples=200,
    centers=2,
    cluster_std=3.5,
    random_state=42,
)

# split the "blog" data
X_train, X_test, y_train, y_test = train_test_split(
    X,
    y,
    test_size=0.50,
    random_state=42,
)

# temporarily create df for easy plotting and printing
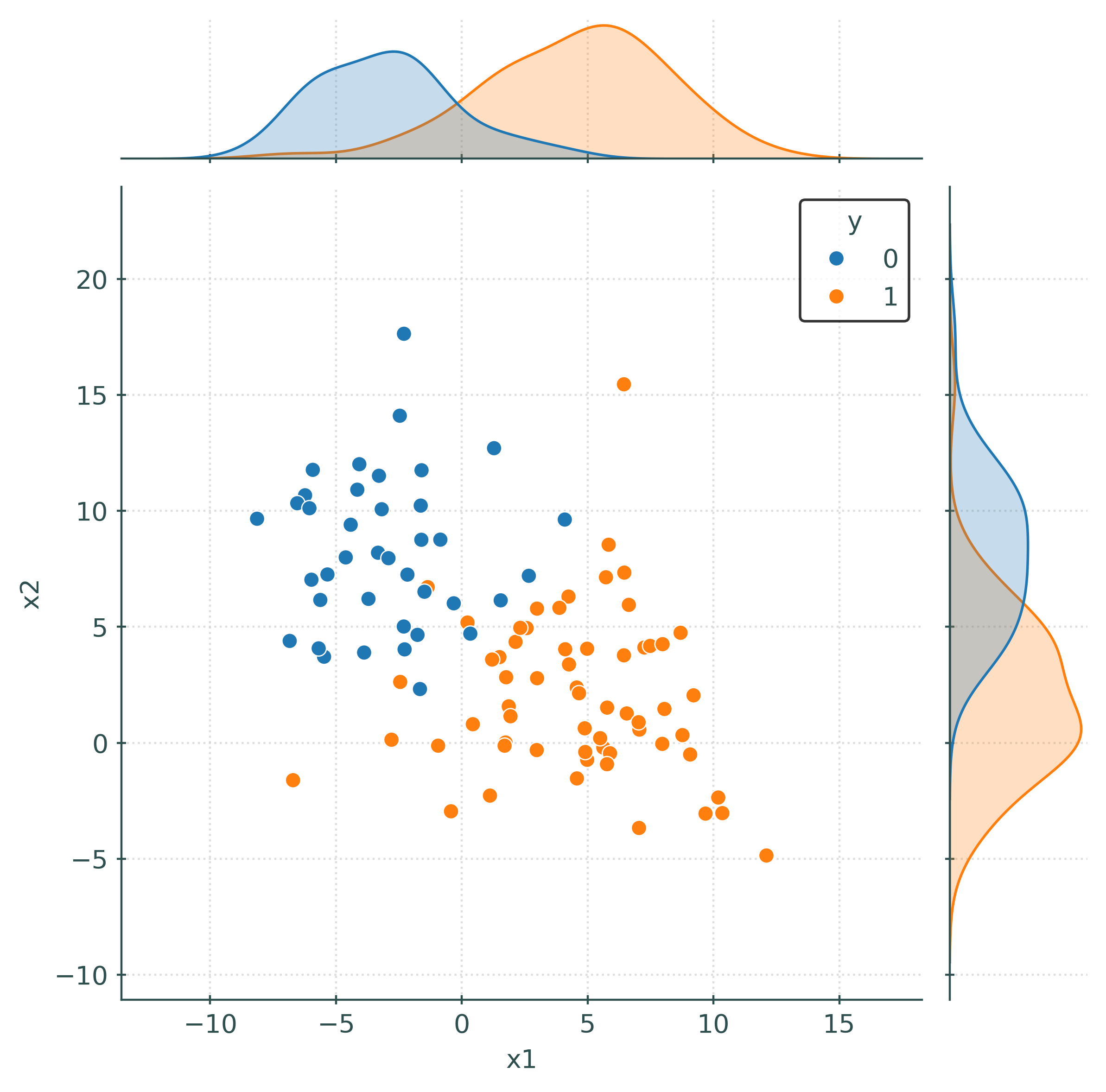
train_df = numpy_to_df(X_train, y_train)
train_df
x1 x2 y
0 5.62 -0.21 1
1 -5.98 7.03 0
2 -5.62 6.16 0
3 -0.43 -2.95 1
4 -8.14 9.66 0
... ... ... ...
95 7.98 4.25 1
96 -6.70 -1.61 1
97 -3.18 10.07 0
98 2.32 4.96 1
99 12.11 -4.86 1

100 rows × 3 columns

# (quickly) create a "joint" plot
_ = sns.jointplot(data=train_df, x="x1", y="x2", hue="y")
plt.show()

In sklearn, unless you set penalty=None, which is not the default, LogisticRegression() is not logistic regression, but rather regularized logistic regression. We will discuss regularized logistic regression in a future note!

# initialize and fit logistic regression
logistic = LogisticRegression(penalty=None)
_ = logistic.fit(X_train, y_train)

# estimated coefficients
logistic.intercept_, logistic.coef_
(array([3.63406579]), array([[ 0.80226887, -0.69174668]]))
# estimated conditional probabilities (first 10 samples from test set)
np.round(logistic.predict_proba(X_test)[range(10)], 3)
array([[0.982, 0.018],
       [0.628, 0.372],
       [1.   , 0.   ],
       [0.992, 0.008],
       [1.   , 0.   ],
       [0.798, 0.202],
       [0.35 , 0.65 ],
       [0.   , 1.   ],
       [1.   , 0.   ],
       [0.012, 0.988]])
# predictions (classifications) on the test data
logistic.predict(X_test)
array([0, 0, 0, 0, 0, 0, 1, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0, 1, 1, 0, 0, 1,
       0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0,
       1, 0, 0, 1, 1, 0, 1, 1, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1, 1, 1, 1,
       1, 0, 0, 0, 0, 0, 1, 1, 0, 0, 1, 0, 0, 0, 1, 1, 0, 0, 0, 1, 1, 0,
       1, 1, 1, 0, 0, 0, 1, 0, 0, 1, 1, 0])
# train accuracy
accuracy_score(y_train, logistic.predict(X_train))


# test accuracy
accuracy_score(y_test, logistic.predict(X_test))
0.92
# plot decision region for initial model
plot_decision_regions(logistic, X_train, y_train)

# create "second order" features (without bias/intercept, it will be "added" later)
poly = PolynomialFeatures(degree=2, include_bias=False)

# "learn" the transformation then apply it to the train and test data
_ = poly.fit(X_train)
X_train_trans = poly.transform(X_train)
X_test_trans = poly.transform(X_test)

# initialize and fit logistic regression with higher order terms
logistic_higher = LogisticRegression(penalty=None)
_ = logistic_higher.fit(X_train_trans, y_train)

# estimated coefficients
logistic_higher.intercept_, logistic_higher.coef_
(array([6.73899122]),
 array([[ 1.22657355, -1.90522748,  0.06187221, -0.0475074 ,  0.07781114]]))
# train accuracy
accuracy_score(y_train, logistic_higher.predict(X_train_trans))
0.96
# test accuracy
accuracy_score(y_test, logistic_higher.predict(X_test_trans))
0.94
# refit the higher-order model using a pipeline
# # this is helpful for plotting decision boundary, also better in practice
pipeline = Pipeline(
    [
        ("poly", PolynomialFeatures(degree=2, include_bias=False)),
        ("logistic", LogisticRegression(penalty=None)),
    ]
)
pipeline.fit(X_train, y_train)
Pipeline(steps=[('poly', PolynomialFeatures(include_bias=False)),
                ('logistic', LogisticRegression(penalty=None))])
In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
# plot decision region for higher-order model
plot_decision_regions(pipeline, X_train, y_train)

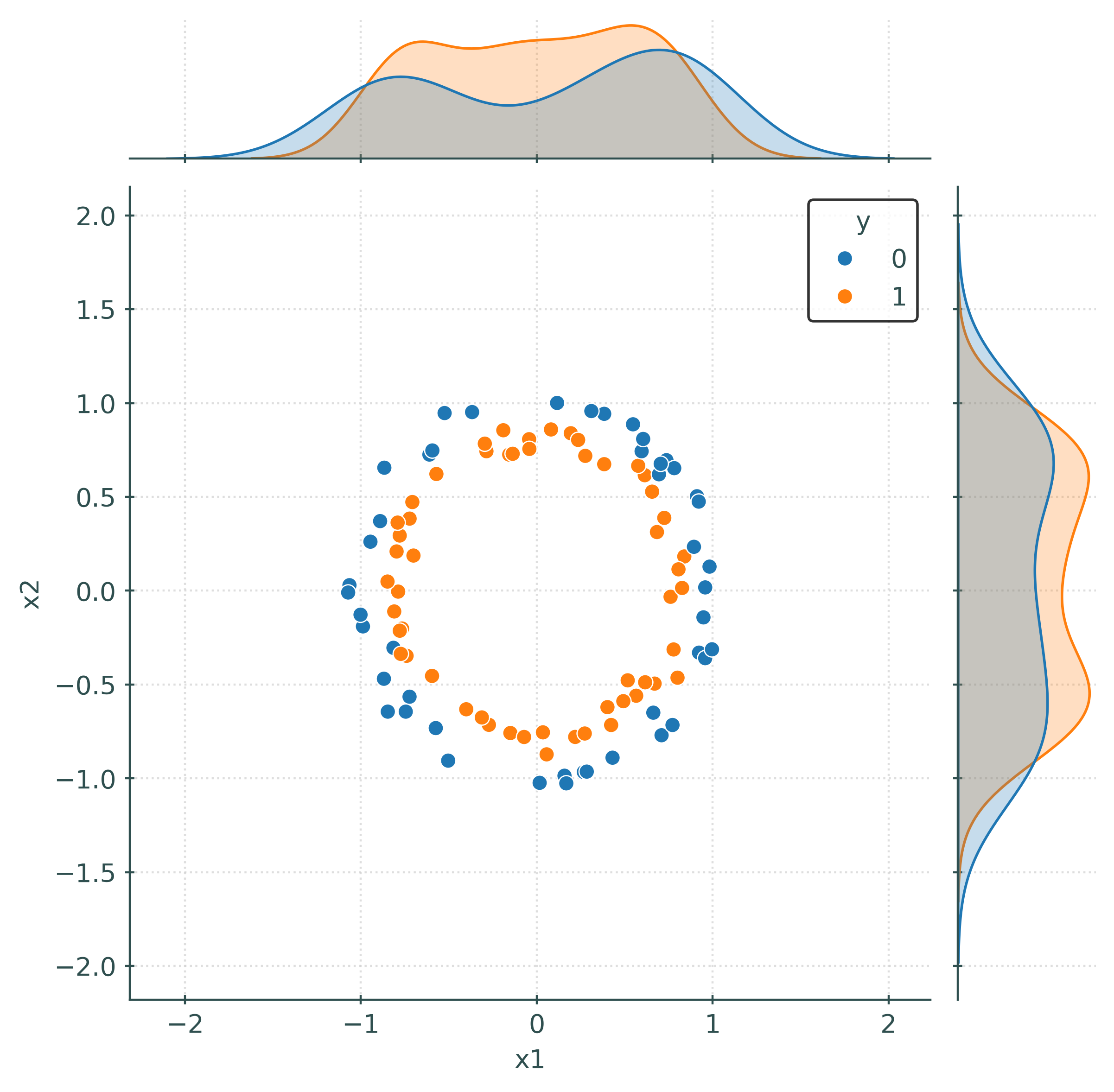
# make and split "circle" data for classification
X, y = make_circles(
    n_samples=200,
    random_state=42,
    noise=0.05,
)
X_train, X_test, y_train, y_test = train_test_split(
    X,
    y,
    test_size=0.50,
    random_state=42,
)
# temporarily create df for easy plotting
train_df = numpy_to_df(X_train, y_train)
train_df
x1 x2 y
0 -0.19 0.86 1
1 -0.81 -0.30 0
2 0.40 -0.62 1
3 -0.52 0.95 0
4 -0.80 0.21 1
... ... ... ...
95 0.70 0.68 0
96 0.49 -0.59 1
97 0.83 0.01 1
98 0.80 -0.46 1
99 -0.79 0.36 1

100 rows × 3 columns

# (quickly) create a "joint" plot
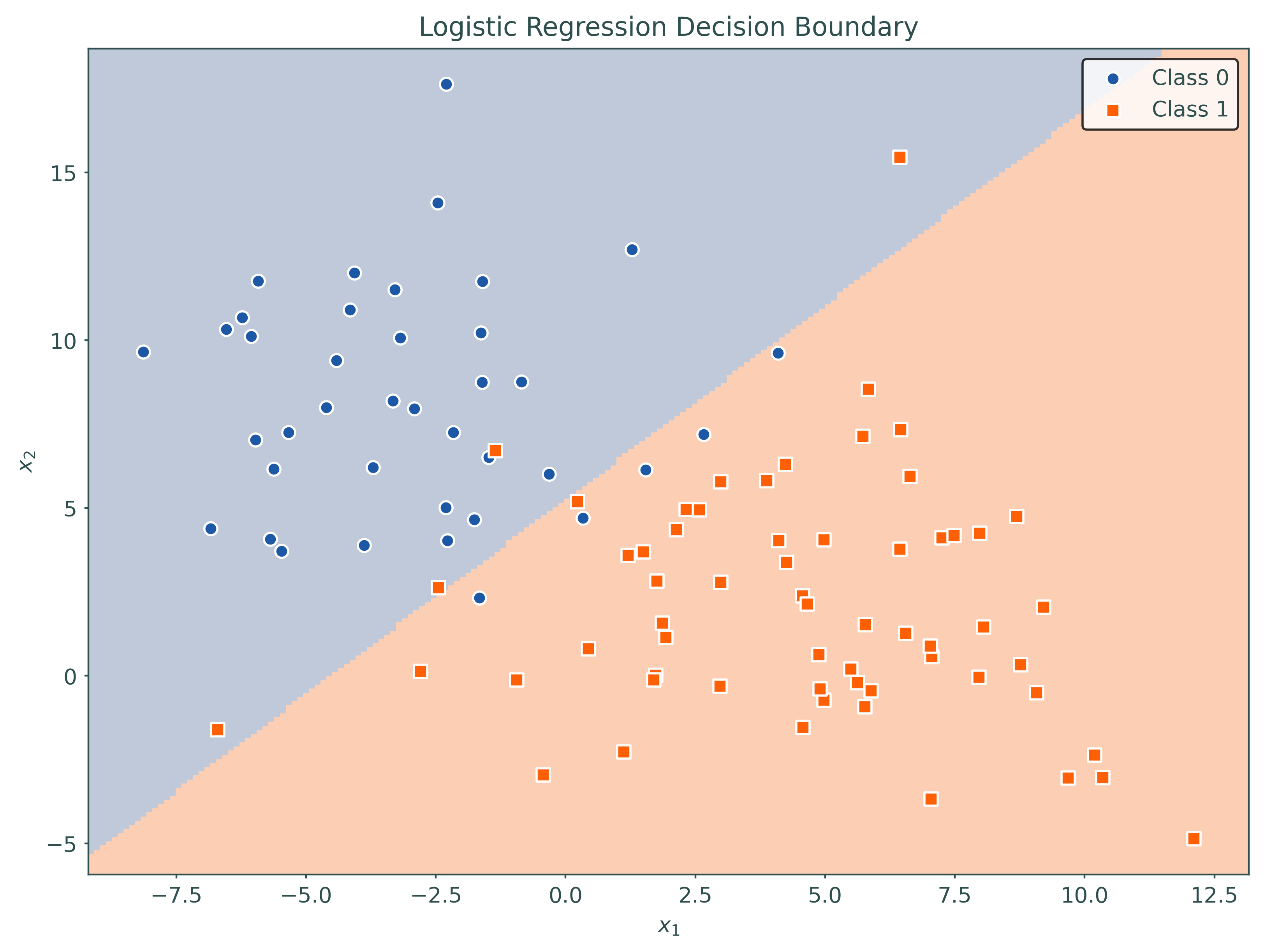
_ = sns.jointplot(data=train_df, x="x1", y="x2", hue="y")
# initialize and fit logistic regression
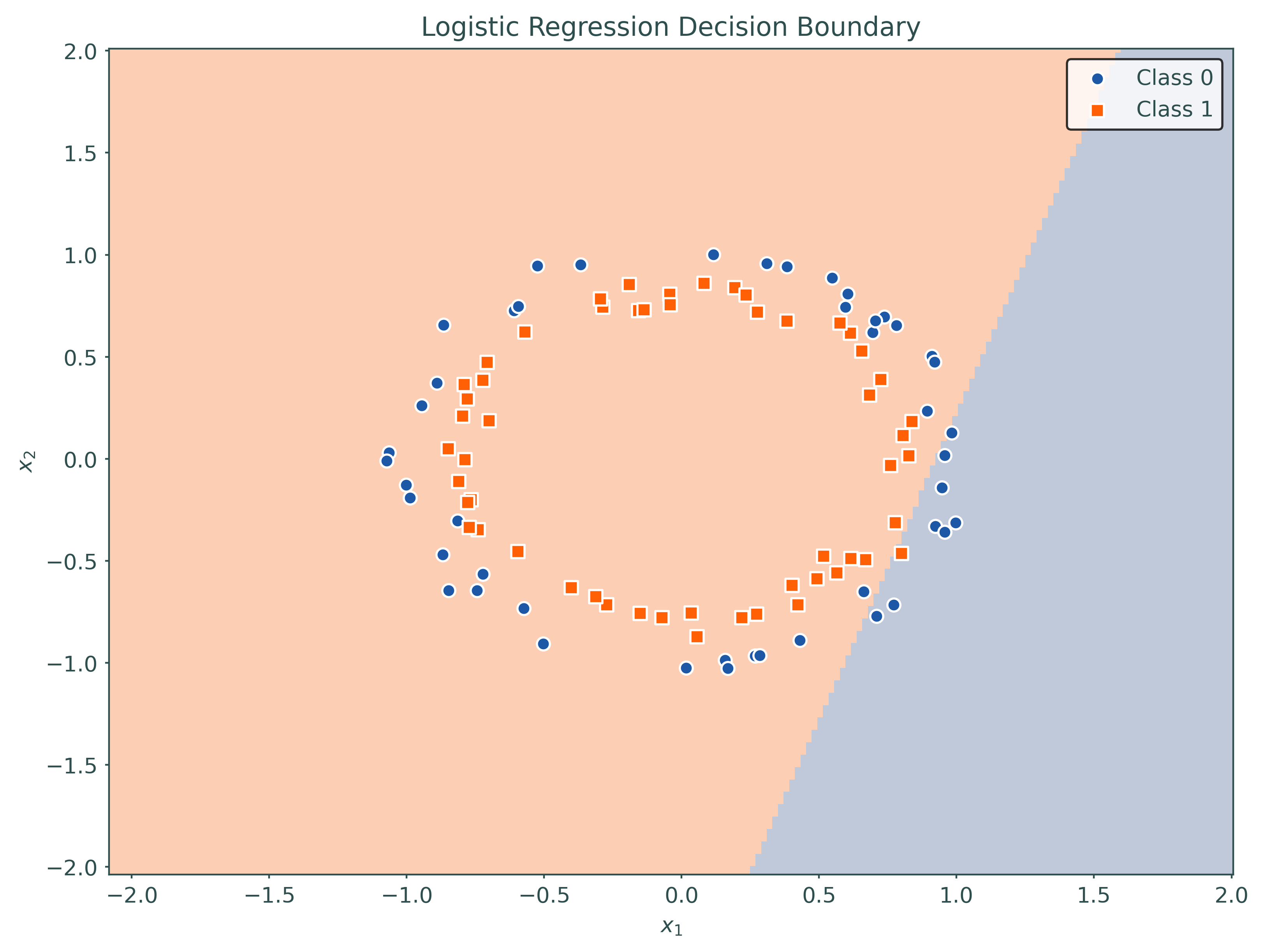
logistic = LogisticRegression(penalty=None)
_ = logistic.fit(X_train, y_train)

# plot decision region for initial model
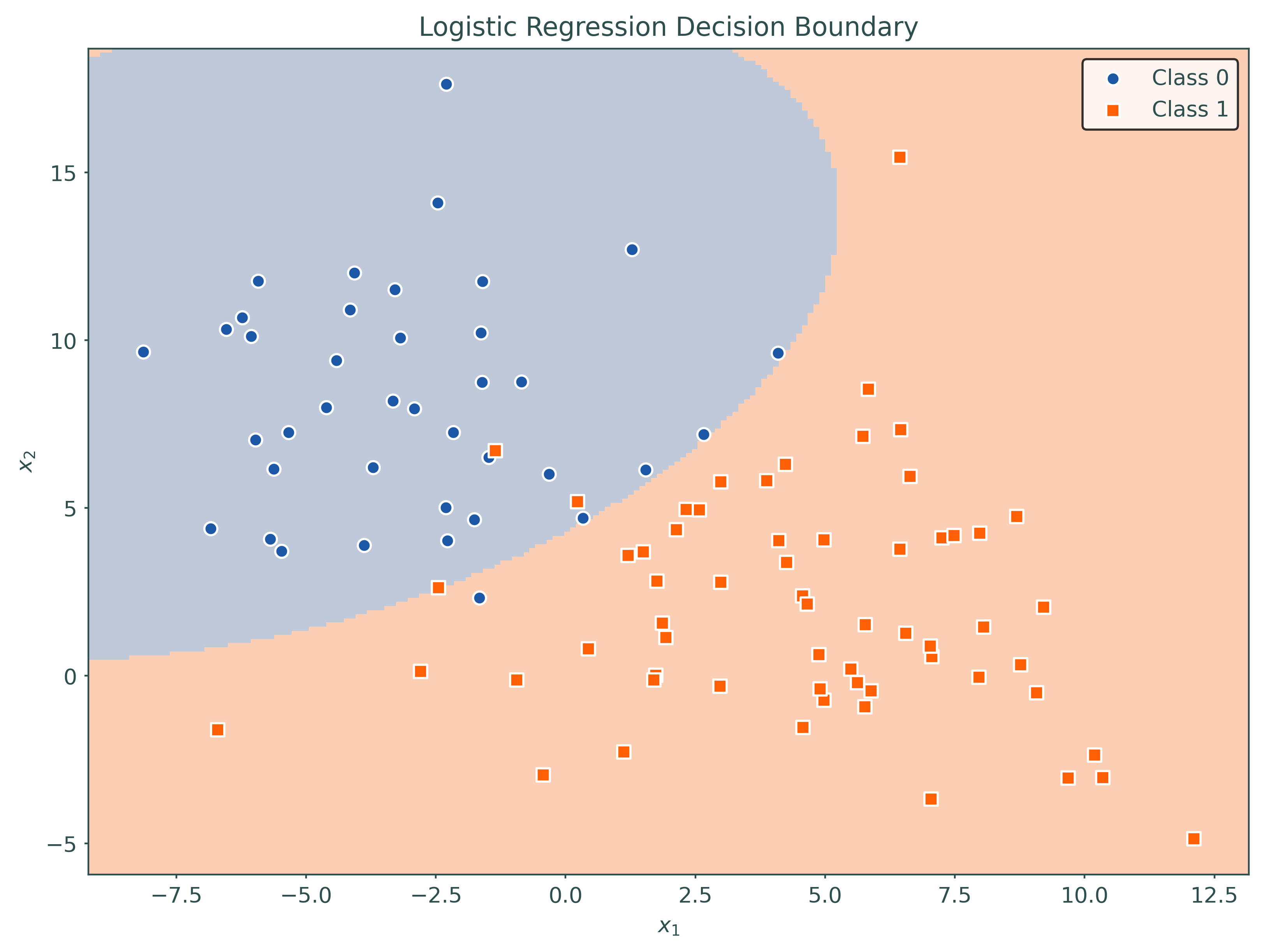
plot_decision_regions(logistic, X_train, y_train)

# setup a higher-order model using a pipeline
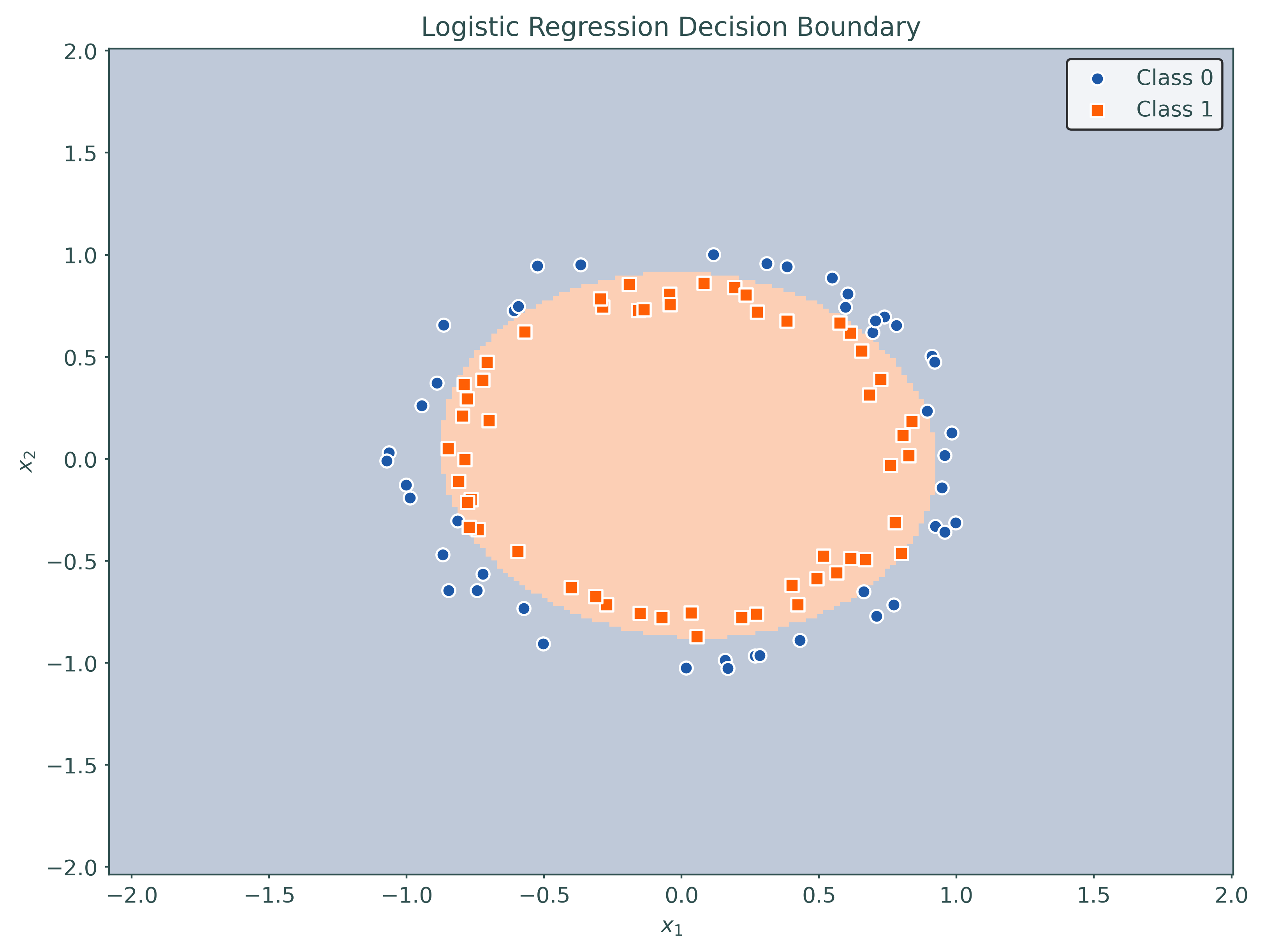
pipeline = Pipeline(
    [
        ("poly", PolynomialFeatures(degree=2, include_bias=False)),
        ("logistic", LogisticRegression(penalty=None)),
    ]
)

# fit a higher-order model using a pipeline
pipeline.fit(X_train, y_train)
Pipeline(steps=[('poly', PolynomialFeatures(include_bias=False)),
                ('logistic', LogisticRegression(penalty=None))])
In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
# plot decision region for higher-order model
plot_decision_regions(pipeline, X_train, y_train)

Footnotes

  1. This is likely true for computer scientists as well, but they also have good reason to use base 2 logarithms.↩︎